P9271 [CEOI 2013] 停车场 / Splot

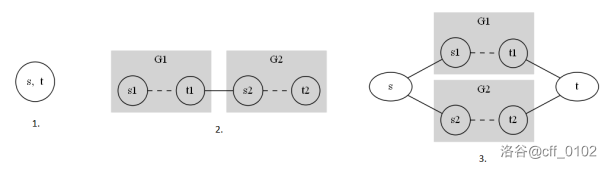
翻译自 [CEOI 2013 Day 1](https://ceoi2013.hsin.hr/tasks/tasks_day1.pdf)。 亚得里亚海沿岸和岛屿都有各种形状和大小的美丽沙滩。然而，许多沙滩无法通过汽车到达。为了满足不断增长的需求，沿海附近的一片巨大空地被改建成停车场。 由于参与设计的所有建筑师都具有电气工程背景，想着怎么着自己学过的专业也得用上，于是停车场的布局就类似于在设计电路时常用的串并联图。 停车场由停车位和连接它们的双向道路组成。每条道路连接两个不同的停车位，每一对停车位之间最多只能通过一条道路连接。每个停车位在任何时刻最多只能停放一辆汽车。其他车辆不能通过被占用的停车位行驶。  $$\text{图 1：构建停车图的规则，对应下面的三点}$$ 串并联停车场（也称为 splot，下文称为停车图）是一种由称为源点和终点的两个特定停车位构成的停车场，它是通过使用串并联组合规则从单个停车位构建而成的。每个停车图可以通过编码来指定其结构和停放车辆的位置，编码是一个描述其结构的字符序列。有效的停车图及其编码按照以下递归方式定义： 1. 只包含一个停车位且没有道路的停车场是一个有效的停车图。这个单个停车位既是停车图的源点也是终点。如果停车位为空，则该停车图的编码为小写字母 `o`，如果停车位被汽车占用，则编码为小写字母`x`。 -  2. 如果 $G_1$ 和 $G_2$ 是两个有效的停车图，它们的串联组合 $G$ 也是一个停车图。串联组合是通过在 $G_1$ 的终点和 $G_2$ 的源点之间添加一条道路来获得的。新获得的停车图 $G$ 的源点是 $G_1$ 的源点，而终点是 $G_2$ 的终点。如果 $E_1$ 和 $E_2$ 分别是停车图 $G_1$ 和 $G_2$ 的编码，则 $G$ 的编码为 `SE1E2#`。换句话说，编码是通过连接大写字母 `S`、组成它的停车图的编码和井号 `#` 获得的。 -  3. 如果 $G_1$ 和 $G_2$ 是两个有效的停车图，它们的并联组合 $G$ 也是一个有效的停车图。并联组合是通过添加两个新的停车位 $s$ 和 $t$，添加从 $s$ 到 $G_1$ 和 $G_2$ 的源之间的道路，以及从 $t$ 到 $G_1$ 和 $G_2$ 的终端之间的道路得到的。新获得的停车图G的源是新添加的停车位 $s$，而 $G$ 的终端是新添加的停车位 $t$。如果 $E_1$ 和 $E_2$ 分别是停车图 $G_1$ 和 $G_2$ 的编码，而 $E_s$ 和 $E_t$ 是源 $s$ 和终端 $t$ 的编码（如果相应的空间为空，则为小写字母 `o`，否则为小写字母 `x`），则 $G$ 的编码为 `PEs|E1E2|Et#`。换句话说，编码是通过连接大写字母 `P`，源停车位的编码，竖线符号 `|`，被组合的停车图的编码，另一个竖线符号 `|`，终端停车位的编码，最后是井号 `#` 得到的。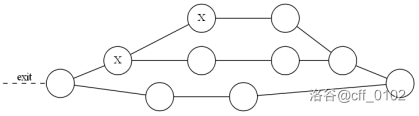 -   $$\text{图2：与下面第一个测试示例对应的停车图}$$ 例如，上图中给出的停车图的编码是 `Po|Px|Sxo#Soo#|o#Soo#|o#`（译者注：`{Po|[Px|(Sxo#)(Soo#)|o#](Soo#)|o#}`）。请注意，停车图 $G$ 的编码中小写字母（`o` 或 `x`）的数量始终与 $G$ 中的停车位数量相同，并且停车图中的停车位与其编码中的小写字母之间存在一一对应关系。停车场只有一个出口，它就在整个停车图的**源停车位**。如果车辆可以通过一些道路和空的停车位到达源停车位，即它可以离开这个停车图，则我们称该车辆未被阻挡。例如，在上面的停车图中，两辆车都没有被阻挡，但是如果我们将一辆车停在停车图的终端（最右边的节点）上，则其中一辆车将被阻挡。允许将车停在停车图的源停车位上（但是如果这样做，停车图中的所有其他车辆都将被阻挡）。

停车场的运营商希望以一种方式安排进站的车辆，让图中没有车辆被阻挡。 编写一个程序，计算可以停放在给定停车场的最大汽车总数，（**包括已经在那里的汽车**），使它没有任何汽车被阻挡，也不会移动任何已经在那里的车。此外，程序应该**找到一种方法**来安排停车图中最大数量的汽车。

输入一行，包含一个至少 $1$ 个、最多 $10$ 万个字符的序列，表示给定的 splot 的编码。序列中只会出现大写字母 `P` 和 `S`，小写字母 `o` 和 `x`，以及字符 `#`（`ASCII 35`）和 `|`（`ASCII 124`）。根据上面的规则，输入将是一个 splot 的编码。输入保证已经在停车场的汽车都不会被阻挡。

输出应包含 $2$ 行。第一行应该包含一个整数 $m$，表示可以停放在 splot 中的最大汽车数量。 第二行应该包含一个字符序列，表示最终将车停放进 splot 的最佳方案。该序列应恰好包含 $m$ 个字母 `x`，并且是通过将原来的一些字母 `o` 替换为 `x` 得来的。 可能有多个最佳安排，程序可以输出其中的任何一个。

样例解释见题目描述最后一趴。 如果输出不正确或不完整，但第一行输出（最大汽车数量）是正确的，你将获得相应测试点 $80\%$ 的分数。 在 $30\%$ 的测试点中，splot 中的停车位总数最多为 $20$ 个。 在另外 $40\%$ 的测试点中，splot 为空，即输入不包含字母 `x`。 对于 $100\%$ 的数据，给定的 splot 的编码最多包含 $10$ 万个字符。 SPJ 提供者：@[cff_0102](https://www.luogu.com.cn/user/542457) 。