P9272 [CEOI 2013] 千岛之国 / Adritic

翻译自 [CEOI 2013 Day 2](https://ceoi2013.hsin.hr/tasks/tasks_day2.pdf)。 “千岛之国”是克罗地亚旅游业在二十世纪九十年代中期的官方口号。虽然这个口号实际上不准确（克罗地亚的岛屿数量略多于 $1000$ 个），但“跳岛旅游”（从一个岛屿航行到另一个岛屿）是一个受欢迎的夏季活动。亚得里亚海的地图是由组成 $2500$ 行和 $2500$ 列的单位正方形组成的网格。行编号从北到南为 $1$ 到 $2500$，而列编号从西到东为 $1$ 到 $2500$。海中有 $N$ 个岛屿，编号为 $1$ 到 $N$，每个岛屿都位于网格的某个单位正方形内。岛屿 $K$ 的位置由相应的网格方格的坐标确定——其行号 $R_K$ 和列号 $C_K$。没有两个岛屿的位置相同。 由于风和海流的影响，只有当岛屿 $B$ 对于 $A$ 来说位于大致的西北或东南方向时才能直接从一个岛屿航行到另一个岛屿。更准确地说，只有在 $R_A < R_B$ 和 $C_A < C_B$ 都成立，或 $R_A > R_B$ 和 $C_A > C_B$ 都成立时，才可以从岛屿 $A$ “跳”到岛屿 $B$。请注意，两个岛屿之间的距离或其他岛屿的存在并不影响从一个岛屿跳到另一个岛屿的可能性。如果无法直接从 $A$ 跳到 $B$，则可能通过其他岛屿使用一些“跳跃”序列从 $A$ 到 $B$ 进行航行。从 $A$ 到 $B$ 的航行距离定义为从 $A$ 到 $B$ 所需的最少“跳跃”次数。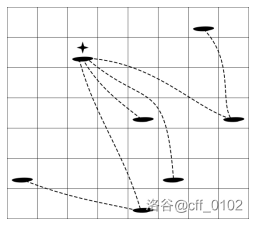  例如，在上面的图中，从位于第 $2$ 行第 $3$ 列的岛屿开始，我们可以跳到另外四个岛屿，而剩下的两个岛屿的航行距离为两个跳跃次数。

一次帆船大会正在计划，组织者正在考虑每个岛屿作为大会的可能场地。在考虑候选岛屿时，他们想知道：如果每个其他岛屿都派出一艘帆船，为了使所有帆船都到达候选岛屿，需要的最小跳数是多少，或者等效地说，从所有其他岛屿到候选岛屿的航行距离之和是多少。 编写一个程序，对于给定 $N$ 个岛屿的位置，对于每个岛屿 $K$，计算所有其他岛屿到岛屿 $K$ 的航行距离之和。测试数据保证，对于所有岛屿 $A$ 和 $B$，可以使用一些跳跃序列从 $A$ 到 $B$ 航行。

第一行包含一个整数 $N$（$1\le N\le250000$），表示岛屿的数量。接下来的 $N$ 行包含岛屿的位置。每个位置用一对整数表示，它们介于 $1$ 和 $2500$ 之间（包括 $1$ 和 $2500$），分别表示行和列号。

输出应包含 $N$ 行。对于每个岛屿，按照它们在输入中给出的顺序，输出从所有其他岛屿到该岛屿的航行距离之和，每个岛屿输出一行。

在 $25\%$ 的测试用例中，$N$ 最多为 $100$。 在 $50\%$ 的测试用例中，$N$ 最多为 $1500$。 在 $60\%$ 的测试用例中，$N$ 最多为 $5000$。 在 $80\%$ 的测试用例中，$N$ 最多为 $25000$。 在 $100\%$ 的测试用例中，$1\le N\le250000$。 **注意：$N$ 可以是 $1$。**