P9296 [POI 2020/2021 R1] Gra platformowa / 平台游戏
题目背景
**题目译自 [XXVIII Olimpiada Informatyczna – I etap](https://sio2.mimuw.edu.pl/c/oi28-1/dashboard/) [Gra platformowa](https://sio2.mimuw.edu.pl/c/oi28-1/p/gra/)。**
题目描述
Bajtazar 正在他的新电脑上玩游戏。
在这个游戏里,有 $n$ 层平台,自上而下分别编号为 $1$ 至 $n$,玩家需要在这些平台之间移动。每层平台的长度为 $X$,因此可以用数对 $(i,x)$ 描述玩家当前的位置,其中 $i$ 表示玩家在第几层平台,$x$ 表示玩家在当前平台的位置(最左端为 $1$,最右端为 $X$)。
玩家从某个平台的最左端开始,游戏的目标是到达任意一个平台的最右端,且玩家只能向右移动。为了增大难度,在平台的一些地方会有洞,这种情况下,玩家可以选择跳跃操作,直接跳过这个洞,也可以通过该洞前往上面或下面的平台,保证不存在两个在水平方向上或竖直方向上相邻的洞。
更具体地说,假如玩家当前的位置为 $(i,x)$,玩家可以执行如下几种操作:
- $\texttt{F}$ 操作:当 $(i,x+1)$ 没有洞时,玩家将会移动到 $(i,x+1)$;否则,玩家将会移动到 $(i+1,x+1)$。
- $\texttt{A}$ 操作:当 $(i,x+1)$ 有洞时,玩家将会移动到 $(i,x+2)$。
- $\texttt{B}$ 操作:当 $(i-1,x)$ 有洞时,玩家将会移动到 $(i-1,x+1)$。
现在 Bajtazar 希望执行最少的跳跃操作(即 $\texttt{A}$ 操作和 $\texttt{B}$ 操作)完成游戏。你能帮他完成这个任务吗?
输入格式
输入第一行三个整数 $n,X,z$,表示一共有 $n$ 层平台,每层平台的长度为 $X$,询问的次数为 $z$。
接下来 $n$ 行,第 $i$ 行描述第 $i$ 层平台的信息。每行开头一个整数 $k_i$,表示该层平台有 $k_i$ 个洞。接下来 $k_i$ 个递增的整数,给出该层每个洞的位置。数据保证任何一个平台的最左端和最右端不存在洞,且不存在两个在水平方向上或竖直方向上相邻的洞。
接下来 $z$ 行,每行包含一个整数 $p_j$,表示在第 $j$ 组询问中,玩家需要从第 $p_j$ 层平台的最左端出发。
输出格式
对于第 $j$ 组询问,请在第 $j$ 行输出一个整数,表示从 $(p_j,1)$ 出发,抵达任意一个平台的最右端需要执行的 $\texttt{A}$ 操作和 $\texttt{B}$ 操作的最小次数。
说明/提示
【样例解释1】:
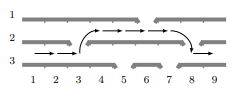
上图给出了样例 $1$ 的第一个询问对应的最优方案:玩家先执行两次 $\texttt{F}$ 操作到达 $(3,3)$,再执行一次 $\texttt{B}$ 操作到达 $(2,4)$,再执行五次 $\texttt{F}$ 操作到达 $(3,9)$。
对于第二个询问,最优方案是执行一次 $\texttt{F}$ 操作,再执行一次 $\texttt{A}$ 操作,最后执行五次 $\texttt{F}$ 操作。
对于第三个询问,最优方案是连续执行八次 $\texttt{F}$ 操作。
【数据范围】:
所有测试点均满足:$1 \leq n \leq 10^5$,$1 \leq X \leq 10^9$,$1 \leq z \leq 10^5$,$\sum k\le 2\times 10^6$。
| 子任务编号 | 约束 | 分值 |
| :-: | :-: | :-: |
|$0$|样例|$0$|
| $1$| $z \leq 5$,$n\times X \leq 10^6$ | $30$ |
| $2$| $z \leq 5$| $50$ |
|$3$| 无附加约束|$20$|