P9315 [EGOI 2021] Angry Cows / 感染的奶牛（暂无数据）

Day 2 Problem C. 题面译自 [EGOI2021 angrycows](https://stats.egoi.org/media/task_description/2021_angrycows_en.pdf)。

近年来，极绿牛病（EGOI）迅速蔓延，这种疾病使奶牛对徒步旅行者产生危险。在发生了几起事故后，人们决定将奶牛饲养区与阿尔卑斯山徒步旅行区分开。 你有一张阿尔卑斯山的地图。地图上有 $n$ 个区域，每个区域都可以是奶牛饲养区、徒步旅行区或未使用区。一些区域之间由双向的小路连接。每条小路都有一个非负的长度。(用图论的术语来说，该地图是一个有边权的无向图）。 你可以在一些地区建墙。一旦你在一个地区建了墙，这个地区就不能让徒步旅行者和奶牛进入了——他们将不再能走过这样的地区。 你的任务是选择放置墙壁的一组区域。这组区域必须满足以下条件： - 它必须只包含未使用的区域。 - 它必须将奶牛饲养区与徒步旅行区分开。也就是说，一头牛无法沿着小路从奶牛饲养区走到徒步旅行区（而不经过有墙的区域）。 - 它**不得**将任何徒步旅行区彼此分开。也就是说，一个徒步旅行者仍然能够沿着小路从任何徒步旅行区走到任何其他徒步旅行区（而不经过有墙的区域）。 如果有多种方法可以达到上述目标，我们会关心墙体的维护是否方便。城墙将由专门的工作人员维护。每个徒步区都有一个这样的工作人员驻扎在那里。 对于任意区域 $A$，定义它的**偏僻度**为它与任何徒步旅行区的最短距离。（路径的长度等于其中每条路的长度之和。请记住，这些路径**可以**穿过墙和奶牛饲养区——工作人员有足够的经验和装备支持他们这么做。） 对于一组区域，它的**偏僻度**为其中每个区域的**最大**偏僻度。 对于所有符合要求的建墙方案，请找出**偏僻度**最小的一个。如果有多个方案符合要求，你可以输出任何一个。 请记住，选择的区域数不做要求。特别地，**并不**要求建立尽量少的墙。

第一行两个整数 $n,m$——区域数和小路数。区域被编号为 $1\sim n$。 第二行 $n$ 个整数 $t_1,\ldots,t_n$，其中 $t_i=-1$ 意味着第 $i$ 个区域是奶牛饲养区，$t_i=0$ 意味着是未使用区，$t_i=1$ 意味着是徒步旅行区。 接下来 $m$ 行，每行三个整数 $a_j,b_j,l_j$，表示有一条连接 $a_j$ 和 $b_j$ 的长度为 $l_j$ 的小路。 数据保证： - 任意两个区域之间最多有一条小路。 - 初始时可以从任何一个区域沿小路走到所有区域。 - 至少有一个奶牛饲养区。 - 至少有一个徒步旅行区。

如果不存在合法方案，输出 $-1$。 否则，第一行一个整数 $k$——你要建的墙数。第二行 $k$ 个整数——你要建墙的区域号。（区域号必须是 $1\sim n$ 内不同的数，可以以任意顺序输出。） 任何一组偏僻度最小的合法方法都将被认为是正确的。

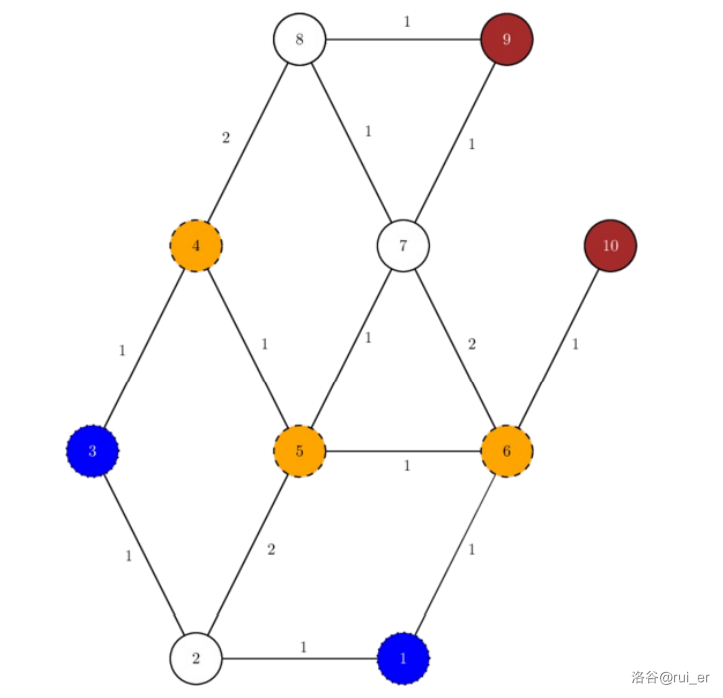
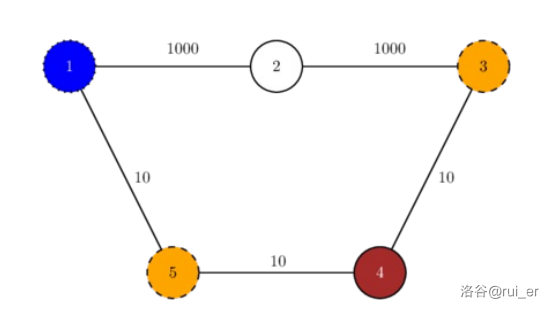
**样例解释的说明** 在所有图中，蓝色（点状边框）标记了徒步旅行区，棕红色（实线边框）标记了奶牛饲养区，橙黄色（短线边框）标记了墙。 --- **样例 $1$ 解释**  最小可能偏僻度为 $2$，在 $4,5,6$ 处建墙即可。注意不能在 $4,2,6$ 处建墙，尽管此时的偏僻度为 $1$，因为这会导致徒步旅行区 $1,3$ 不连通。 --- **样例 $2$ 解释**  区域 $2$ 的偏僻度为 $10^3$，区域 $3$ 的偏僻度为 $30$，因为它可以从 $1-5-4-3$ 被到达。（请回忆，工作人员可以穿过墙和奶牛饲养区。）因此我们应该在 $5$ 和 $3$（而不是 $2$）处建墙，此时偏僻度为 $30$。 --- **数据范围** 对于全部数据，$2\le n\le 3\times 10^5$，$n-1\le m\le 3\times 10^5$，$t_i\in\{-1,0,1\}$，$1\le a_j < b_j\le n$，$0\le l_j\le 10^9$。 - 子任务一（$7$ 分）：$n\le 10$。 - 子任务二（$22$ 分）：$l_j=0$。 - 子任务三（$16$ 分）：恰有一个徒步旅行区。 - 子任务四（$11$ 分）：有 $n-1$ 条小路（用图论的术语来说，该图是一棵树）。 - 子任务五（$8$ 分）：$n,m\le 2\times 10^3$，$l_j=1$。 - 子任务六（$36$ 分）：无特殊限制。