P9322 [EGOI 2022] Superpiece / 超级棋子

Day 2 Problem B. 题面译自 [EGOI2022 superpiece](https://stats.egoi.org/media/task_description/2022_superpiece_en.pdf)。 [](https://creativecommons.org/licenses/by-sa/3.0/)

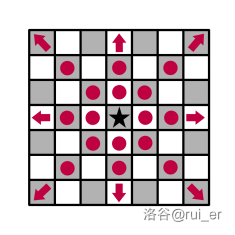
你有一个无限大的棋盘。在本题中，棋盘是一个无限大的二维方格，每个方格用 $(r,c)$ 表示，分别代表行和列。目前棋盘上有唯一一个棋子，叫做**超级棋子**。你有你的超级棋子的合法移动列表，它是一个非空字符串，是 `QRBNKP` 的子序列。在每个回合中，超级棋子可以作为给定的棋子之一移动。超级棋子初始位于 $(a,b)$，请求出到达 $(c,d)$ 的最少移动次数。 在本题中可能用到的国际象棋规则如下： 共有六种棋子：皇后、车、象、马、国王、兵。他们的移动方式如下： - **皇后**（`Q`）可以移动到同行、同列、同对角线的方格。形式化地，对于任意整数 $k\ne 0$，皇后可以从 $(a,b)$ 移动到 $(a+k,b),(a,b+k),(a+k,b+k),(a+k,b-k)$。  - **车**（`R`）可以移动到同行、同列的方格。形式化地，对于任意整数 $k\ne 0$，车可以从 $(a,b)$ 移动到 $(a+k,b),(a,b+k)$。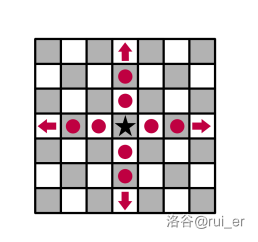  - **象**（`B`）可以移动到同对角线的方格。形式化地，对于任意整数 $k\ne 0$，象可以从 $(a,b)$ 移动到 $(a+k,b+k),(a+k,b-k)$。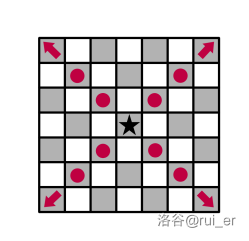  - **马**（`N`）可以移动一个 `L` 形，也就是：先在一个方向移动两格，再在与之垂直的方向移动一格。形式化地，马可以从 $(a,b)$ 移动到 $(a+1,b+2),(a+1,b-2),(a+2,b+1),(a+2,b-1),(a-2,b+1),(a-2,b-1),(a-1,b+2),(a-1,b-2)$。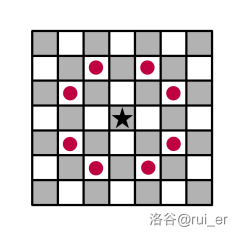  - **国王**（`K`）可以移动到相邻的八个格子。形式化地，国王可以从 $(a,b)$ 移动到 $(a,b+1),(a,b-1),(a+1,b),(a-1,b),(a+1,b+1),(a+1,b-1),(a-1,b+1),(a-1,b-1)$。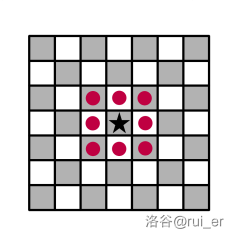  - **兵**（`P`）可以向上移动一格。形式化地，兵可以从 $(a,b)$ 移动到 $(a+1,b)$。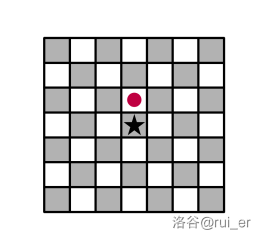  请注意，你可能知道的关于国际象棋的其他规则并不适用于本题；请只使用上面列出的那些规则。

第一行一个整数 $q$，表示数据组数。之后每两行描述一组数据： - 每组数据的第一行一个非空字符串，是超级棋子的合法移动列表。这个字符串是 `QRBNKP` 的一个子集，所有字符**按相同顺序**出现。换句话说，它是 `QRBNKP` 的一个子序列。 - 每组数据的第二行四个整数 $a,b,c,d$——超级棋子的初始和目标位置。保证 $(a,b)\ne (c,d)$，也就是初始位置和目标位置不同。

对于每组数据，输出一行一个整数 $m$，表示最少移动次数。如果不可能到达目标位置，输出 $-1$。

**样例 $1$ 解释** 在第一组数据中，我们需要从 $(3,3)$ 走到 $(5,1)$，合法移动有马、国王、兵。有很多种需要两次移动的方案，例如： - 兵走到 $(4,3)$，马走到 $(5,1)$。 - 马走到 $(5,2)$，国王走到 $(5,1)$。 - 国王走到 $(4,2)$，国王走到 $(5,1)$。 不存在少于两次移动的方案——我们需要象或者皇后才能做到。 在第二组数据中，我们需要从 $(2,6)$ 走到 $(5,3)$。同样地，最优方案需要两次移动。此时，每一步都必须是马，利用 $(4,5)$ 或 $(3,4)$ 作为中转站。 --- **样例 $2$ 解释** 在第一组数据中，我们需要从 $(2,8)$ 走到 $(3,6)$。只能按照象的方式走棋，这是不可能的。 在第二组数据中，我们需要从 $(2,8)$ 走到 $(5,5)$，只能按照象的方式走棋。可以在两次移动内实现，例如，利用 $(4,4)$ 作为中转站。 --- **样例 $3$ 解释** 在第一组数据中，我们需要从 $(3,3)$ 走到 $(4,5)$，只能按照皇后的方式走棋。可以利用 $(4,4)$ 为中转站两次移动到达。 在第二组数据中，我们需要从 $(4,1)$ 走到 $(1,4)$，只能按照皇后和车的方式走棋。可以一次移动到达。 --- **数据范围** 对于全部数据，$1\le q\le 10^3$，$-10^8\le a,b,c,d\le 10^8$。 - 子任务一（$12$ 分）：保证存在 `Q`，保证不存在 `N`。 - 子任务二（$9$ 分）：保证存在 `QN`。 - 子任务三（$13$ 分）：保证存在 `R`，保证不存在 `Q`。 - 子任务四（$8$ 分）：保证只存在 `B`。 - 子任务五（$6$ 分）：保证存在 `B`，保证不存在 `QR`。 - 子任务六（$31$ 分）：保证只存在 `N`。 - 子任务七（$8$ 分）：保证存在 `N`，保证不存在 `QRB`。 - 子任务八（$7$ 分）：保证存在 `K`，保证不存在 `QRBN`。 - 子任务九（$6$ 分）：保证只存在 `P`。 注意子任务**并不**按难度顺序排序。