P9328 [CCC 2023 S5] The Filter

Alice, the mathematician, likes to study real numbers that are between $0$ and $1$. Her favourite tool is the filter. A filter covers part of the number line. When a number reaches a filter, two events can happen. If a number is not covered by the filter, the number will pass through. If a number is covered, the number will be removed. Alice has infinitely many filters. 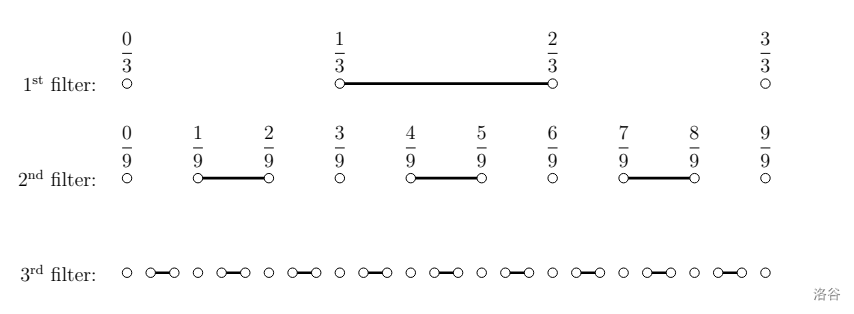Her first $3$ filters look like this:  In general, the $k\text{-th}$ filter can be defined as follows: - Consider the number line from $0$ to $1$. - Split this number line into $3^k$ equal-sized pieces. There are $3^k + 1$ points and $3^k$ intervals. - The $k\text{-th}$ filter consists of the $2^{\text{nd}}$ interval, $5^{\text{th}}$ interval, $8^{\text{th}}$ interval, and in general, the $(3i-1)^{\text{th}}$ interval. The points are **not** part of the $k\text{-th}$ filter. Alice has instructions for constructing the Cantor set. Start with the number line from $0$ to $1$. Apply all filters on the number line, and remove the numbers that are covered. The remaining numbers form the Cantor set. Alice wants to research the Cantor set, and she came to you for help. Given an integer $N$, Alice would like to know which fractions $\frac{x}{N}$ are in the Cantor set.

The first line contains the integer $N$. The following table shows how the available $15$ marks are distributed. | Marks | Bounds on $N$ | Additional Constraints | | :----------: | :----------: | :----------: | | $3$ marks | $3 \leq N \leq 3^{18}$ | $N$ is a power of $3$. | | $4$ marks | $2 \leq N \leq 2 \times 10^5$ | None. | | $8$ marks | $2 \leq N \leq 2 \times 10^9$ | None. |

Output all integers $x$ where $0 \leq x \leq N$ and $\frac{x}{N}$ is in the Cantor set. Output the answers in increasing order. The number of answers will not exceed $10^6$.

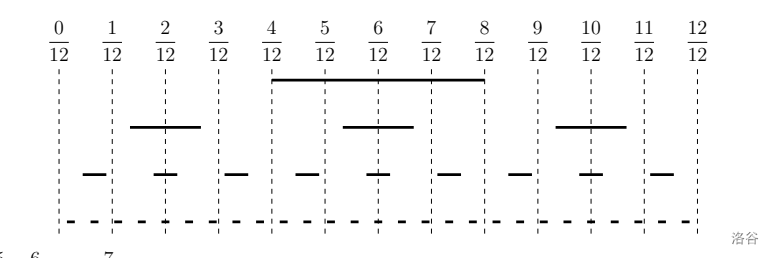
 $\frac{5}{12},\frac{6}{12},\frac{7}{12}$ are not in the Cantor set because they were covered by the 1st filter. Furthermore, $\frac{2}{12}$ and $\frac{10}{12}$ are not in the Cantor set because they were covered by the $2^{\text{nd}}$ filter. It can be shown that the remaining fractions will pass through all filters. **本题采用捆绑测试**： - Subtask 1（3 points）：$3 \leq N \leq 3 ^{18}$，$N$ 是 $3$ 的整数次幂。 - Subtask 2（4 points）：$2 \leq N \leq 2\times 10^5$。 - Subtask 3（8 points）：$2 \leq N \leq 2 \times 10^9$。