P9328 [CCC 2023 S5] The Filter

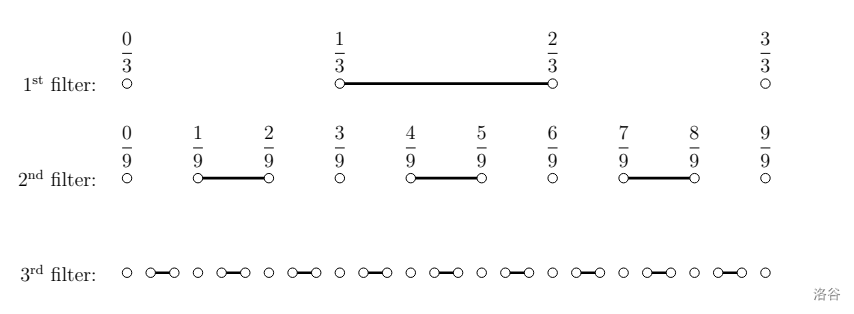
数学家 Alice 喜欢研究介于 $0$ 和 $1$ 之间的实数。她最喜欢的工具是滤器。 滤器覆盖数轴的一部分。当一个数字到达滤器时，会发生两种情况。如果一个数字没有被滤器覆盖，则该数字将通过。如果一个数字被覆盖，则该数字将被移除。 Alice 有无数个滤器。她的前三个滤器如下所示：  一般来说，第 $k$ 个滤器可以定义如下： - 考虑从 $0$ 到 $1$ 的数轴。 - 将这个数轴分成 $3^k$ 个等大小的部分。有 $3^k + 1$ 个点和 $3^k$ 个区间。 - 第 $k$ 个滤器由第 $2$ 个区间、第 $5$ 个区间、第 $8$ 个区间组成，一般来说，是第 $(3i-1)$ 个区间。这些点**不**是第 $k$ 个滤器的一部分。 Alice 有构造 Cantor 集合的说明。首先从 $0$ 到 $1$ 的数轴开始。对数轴应用所有滤器，并移除被覆盖的数字。剩下的数字形成 Cantor 集合。 Alice 想研究 Cantor 集合，她来找你帮忙。给定一个整数 $N$，Alice 想知道哪些分数 $\frac{x}{N}$ 在 Cantor 集合中。

第一行包含整数 $N$。 下表显示了可用的 $15$ 分的分布情况。 | 分数 | $N$ 的范围 | 额外约束 | | :----------: | :----------: | :----------: | | $3$ 分 | $3 \leq N \leq 3^{18}$ | $N$ 是 $3$ 的幂。 | | $4$ 分 | $2 \leq N \leq 2 \times 10^5$ | 无。 | | $8$ 分 | $2 \leq N \leq 2 \times 10^9$ | 无。 |

输出所有整数 $x$，其中 $0 \leq x \leq N$ 且 $\frac{x}{N}$ 在 Cantor 集合中。 按递增顺序输出答案。答案的数量不会超过 $10^6$。

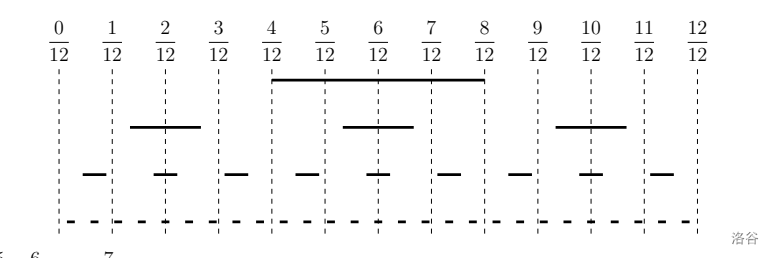
 $\frac{5}{12},\frac{6}{12},\frac{7}{12}$ 不在 Cantor 集合中，因为它们被第一个滤器覆盖。此外，$\frac{2}{12}$ 和 $\frac{10}{12}$ 不在 Cantor 集合中，因为它们被第二个滤器覆盖。 可以证明，剩下的分数将通过所有滤器。 **本题采用捆绑测试**： - 子任务 1（3 分）：$3 \leq N \leq 3 ^{18}$，$N$ 是 $3$ 的整数次幂。 - 子任务 2（4 分）：$2 \leq N \leq 2\times 10^5$。 - 子任务 3（8 分）：$2 \leq N \leq 2 \times 10^9$。 题面翻译由 ChatGPT-4o 提供。