P9341 [JOIST 2023] Security Guard

In JOI Kingdom, there are $N$ islands, numbered from $1$ to $N$. Each island has the insecurity level. The insecurity level of the island $i\ (1 \le i \le N)$ is $S_i$. In JOI Kingdom, ships between pairs of islands are mostly used as the methods of transportations. There are $M$ ships, numbered from $1$ to $M$. The ship $j\ (1 \le j \le M)$ connects the island $A_j$ and the island $B_j$. We can run ships when necessary. It is possible to travel from any island to any other island by taking a number of ships. In JOI Kingdom, there is a plan to introduce new ships. We can choose any pairs of islands where newly introduced ships connect. One day, an incident occurred. A ship at anchor was attacked. Prime minister K of JOI Kingdom decided to introduce new ships. He also demands that ships in JOI Kingdom should satisfy the following **Security Condition**. - When a ship is anchored at the island $i\ (1 \le i \le N)$, the number of security guards on the ship is greater than or equal to $S_i$. However, since it is expensive to hire security guards, we want to minimize the number of hired security guards. As long as the condition “it is possible to travel from any island to any other island by taking a number of ships” is satisfied, it is possible to abolish ships which are currently running. Therefore, we will run ships as follows. Here, $k$ is the number of newly introduced ships. 1. For each of the $k$ newly introduced ships, we choose two islands where it connects. 2. We choose a number of (more than or equal to $0$) ships, and we abolish them. It is allowed to abolish newly introduced ships. 3. For each of the ships, we anchor it at one of the two islands where it connects. We make a number of security guards get on it. Moreover, the following conditions should be satisfied. *Condition*     For every pair $u, v\ (1 \le u \le N, 1 \le v \le N)$ of islands, it is possible to transport a passenger from the island $u$ to the island $v$ by repeating the following operations a number of times. In the process, Security Condition should be satisfied all the time. - We make a passenger or security guards get on a ship which is anchored at the island where the passenger or security guards are staying. - We make a passenger or security guards get off a ship at the island where the ship is currently anchored. - We move a ship from the island where the ship is currently anchored to the other island where the ship connects. Since the budget is limited, we can introduce at most $Q$ new ships. For each $k\ (0 \le k \le Q)$, Prime minister K wants to know the minimum possible number of hired security guards if the number of newly introduced ships is $k$. Write a program which, given the information of islands and the routes of the ships and the number of new ships we can introduce, calculates the minimum possible number of hired security guards for each $k$.

Read the following data from the standard input. > $N\ M\ Q$ > > $S_1\ S_2\ \cdots\ S_N$ > > $A_1\ B_1$ > > $A_2\ B_2$ > > $\vdots$ > > $A_M\ B_M$

Write $Q+1$ lines to the standard output. The $(k+1)$-th line $(0 \le k \le Q)$ of output should contain the minimum possible number of hired security guards if the number of newly introduced ships is $k$.

#### 【样例解释 #1】 If the number of newly introduced ships is $0$, we need $7$ security guards. For example, the conditions are satisfied if we allocate the ships and $7$ security guards as follows. - The ship $1$ is initially anchored at the island $2$, and two security guards get on the ship $1$. - The ship $2$ is initially anchored at the island $2$, and two security guards get on the ship $2$. - The ship $3$ is initially anchored at the island $4$, and three security guards get on the ship $3$. Let us explain how to transport a passenger in the following two cases. - We transport a passenger from the island $1$ to the island $4$. - We transport a passenger from the island $3$ to the island $2$. We can transport a passenger from the island $1$ to the island $4$ as follows. The islands where the ships $1, 2, 3$ are anchored, and the numbers of security guards on the ships $1, 2, 3$ are written in this order. The numbers of security guards on the islands $1, 2, 3, 4$ are written in this order.  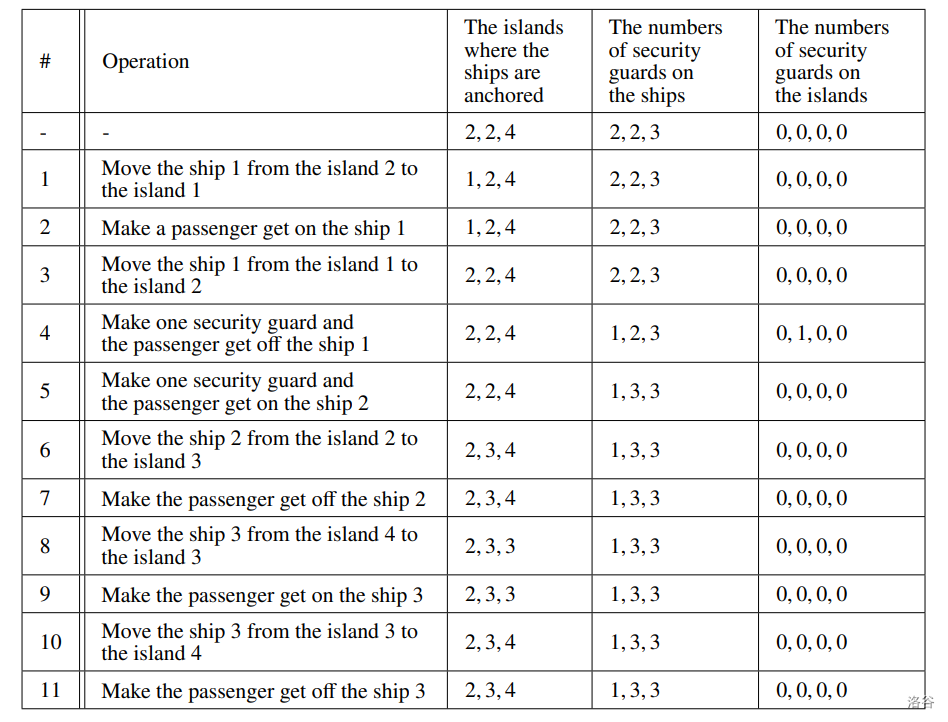We can transport a passenger from the island $3$ to the island $2$ as follows.  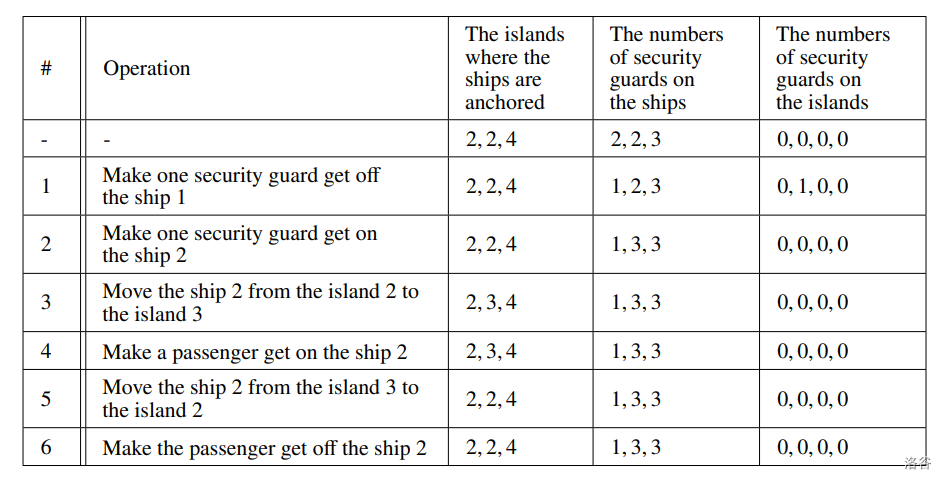Since it is impossible to satisfy the conditions if the number of security guards is less than or equal to $6$, output $7$. This sample input satisfies the constraints of Subtasks $2, 3, 4, 5, 6, 7$. #### 【样例解释 #2】 If the number of newly introduced ships is $0$, similarly as Sample Input $1$, we need $7$ security guards. If the number of newly introduced ships is $1$, we need $5$ security guards. For example, the conditions are satisfied if we allocate the ships and $5$ security guards as follows. - We introduce a new ship connecting the island $2$ and the island $4$. (In the following, we call it the ship $4$.) - We abolish the ship $3$. - We initially anchor the ship $1$ at the island $2$, and make two security guards get on the ship $1$. - We initially anchor the ship $2$ at the island $2$, and make one security guard get on the ship $2$. - We initially anchor the ship $4$ at the island $2$, and make two security guards get on the ship $4$. This sample input satisfies the constraints of Subtasks $5, 6, 7$. #### 【样例解释 #3】 If the number of newly introduced ships is $0$, we need $2$ security guards. For example, the conditions are satisfied if we allocate the ships and $2$ security guards as follows. - We abolish the ship $3$. - We initially anchor the ship $1$ at the island $1$, and make one security guard get on the ship $1$. - We initially anchor the ship $2$ at the island $1$, and make one security guard get on the ship $2$. This sample input satisfies the constraints of Subtasks $4, 5, 6, 7$. #### 【样例解释 #4】 This sample input satisfies the constraints of all the subtasks. #### 【样例解释 #5】 This sample input satisfies the constraints of Subtasks $3, 4, 5, 6, 7$. #### 【样例解释 #6】 This sample input satisfies the constraints of Subtasks $5, 6, 7$. #### 【数据范围】 对于所有测试数据，满足： - $2 \le N \le 2\times 10 ^ 5$; - $N - 1 \le M \le 4\times 10 ^ 5$; - $0 \le Q \le 2\times 10 ^ 5$; - $1 \le S_i \le 10 ^ 9\ (1 \le i \le N)$; - $1 \le A_j < B_j \le N\ (1 \le j \le M)$; - $(A_x, B_x) \neq (A_y, B_y)\ (1 \le x < y \le M)$; - It is possible to travel from any island to any other island by taking a number of ships; - Given values are all integers. | 子任务编号 | 分值 | 特殊限制 | | :----------: | :----------: | :----------: | | $1$ | $12$ | $M = N - 1$，$Q = 0$，$S_i \le 2\ (1 \le i \le N)$，$A_j = j$，$B_j = j + 1\ (1 \le j \le M)$ | | $2$ | $13$ | $M = N - 1$，$Q = 0$，$A_j = j$，$B_j = j + 1\ (1 \le j \le M)$ | | $3$ | $12$ | $M = N - 1$，$Q = 0$ | | $4$ | $13$ | $Q = 0$ | | $5$ | $8$ | $N \le 16$ | | $6$ | $18$ | $N \le 3 000$ | | $7$ | $24$ | 无 |