P9399 「DBOI」Round 1 人生如树

> _永远这么酷 永远永远这么酷_\ _像个冒险家一样 不断探着山顶的路_\ ——《Hustle》 张均好望着窗外，朱芝心走过来坐在他旁边，折了一架纸飞机飞出去。他对张均好说，要带着对未来的期待，往前走，别回头。 正如 [命运](https://www.luogu.com.cn/problem/P6773) 所述，每个人的人生都是一棵树。它总在无限的随机与缘分中伸展，有的枝丫茂盛了，有些却也不可避免地枯萎。

朱芝心用魔法得到了张均好的人生树。 这是一棵 $n$ 个节点的树，节点 $i$ 上有权值 $w_i$。 朱芝心想要观测 $m$ 次张均好的人生： 设**当前**张均好人生树上的节点数量为 $s$。 1. 输入四个整数 $u_1,v_1,u_2,v_2$。令 $u_1\to v_1$ 的简单路径上**顺次组成**的数组为 $a$，$u_2\to v_2$ 的简单路径上**顺次组成**的数组为 $b$。朱芝心认为张均好这两段人生的相似度是 $LRP(a,b)$，希望你求出它。保证 $1\leq u_1,v_1,u_2,v_2 \leq s$。 2. 输入两个整数 $u,w'$。朱芝心观测到了张均好的另外一种可能，因此你需要新建一个点权为 $w'$ 的节点，编号为 $s+1$，建立一条 $(s+1,u)$ 的无向边，其中 $u\leq s$。显然，此后 $s\leftarrow s+1$。 对于两个数组 $a,b$，设它们的相似度 $LRP(a,b)$ 表示最大的 $i$ 满足 $i\leq \min\{|a|, |b|\}$ 且**对于所有** $1\leq j\leq i$，都有 $b_j=a_j+j$。其中 $|a|$ 表示数组 $a$ 的长度。特殊地，若不存在这样的 $i$，则 $LRP(a,b) = 0$。

第一行三个正整数 $n,m,idx$，分别表示树的节点数量，操作数量和该测试点所在 Subtask 编号。对于样例，有 $idx = 0$。 接下来一行 $n$ 个整数，第 $i$ 个整数表示 $w_i$，即点 $i$ 上的权值。 接下来 $n - 1$ 行，每行两个正整数 $u_i,v_i$，表示有一条 $(u_i,v_i)$ 的无向边。 接下来 $m$ 行，每行一个操作。每行第一个整数是 $opt$，后面的若干整数表示操作的具体内容。$opt=1$ 时表示是操作 $1$，$opt=2$ 时表示是操作 $2$。

对于每个操作 $1$，输出一行，表示当前询问的 $LRP(a, b)$。

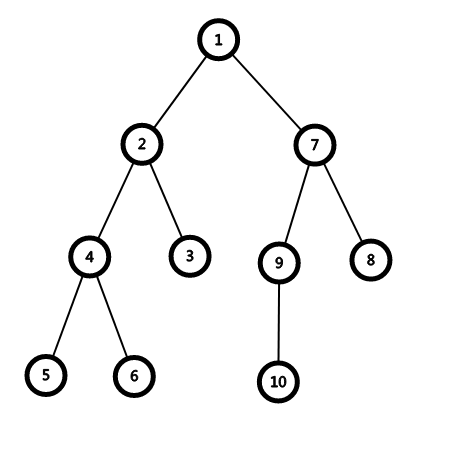
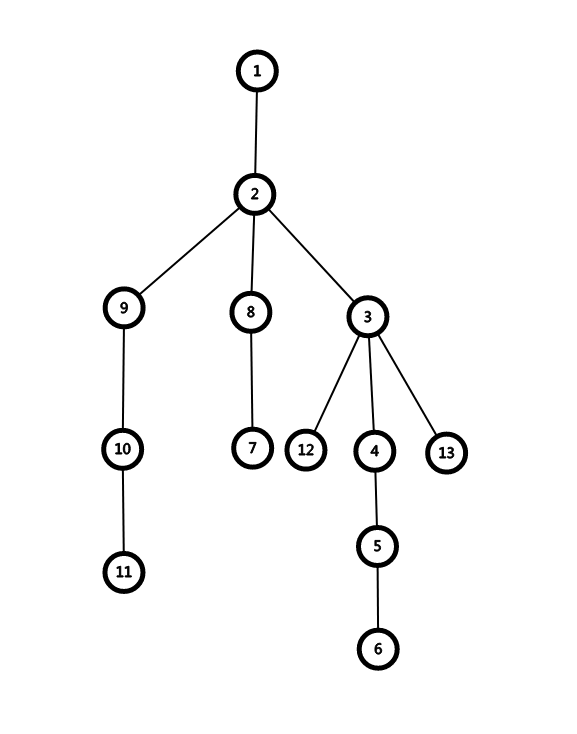
### 样例解释 对于样例一，第一个操作结束后，$w_{10}=10$，树如图所示：  - 对于第二个操作，第一条路径为 $3\to 2\to 4\to 5$，故 $a=\{2, 3, 4, 6\}$，第二条路径为 $8\to 7\to 9\to 10$，故 $b=\{3, 5, 7, 10\}$，由于 $3=2+1$，$5=3+2$，$7=4+3$，$10=6+4$，所以答案为 $4$； - 对于第三个操作，$a=\{2, 3, 4, 5\}$，$b=\{3, 5, 7, 10\}$，由于 $3=2+1$，$5=3+2$，$7=4+3$，$10\ne 5+4$，所以答案为 $3$。 对于样例二，初始的树如图所示：  | Subtask | $n \le$ | $m \le$ | 特殊性质 | 分值 | | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | | Subtask 1 | $5000$ | $5000$ | 无 | $10$ | | Subtask 2 | $10^5$ | $5\times{10}^4$ | A & B | $30$ | | Subtask 3 | $10^5$ | $5\times{10}^4$ | B | $30$ | | Subtask 4 | $10^5$ | $5 \times {10}^4$ | 无 | $20$ | | Subtask 5 | $10^5$ | $10^5$ | 无 | $10$ | 特殊性质 A：$v_i=u_i+1$。 特殊性质 B：保证无操作 2。 对于 $100\%$ 的数据，$1\leq n,m\leq 10^5$，$1\leq w_i,w'\leq 10^6$，$1\leq u_i,v_i\leq n$。