P9415 「NnOI R1-T4」下楼

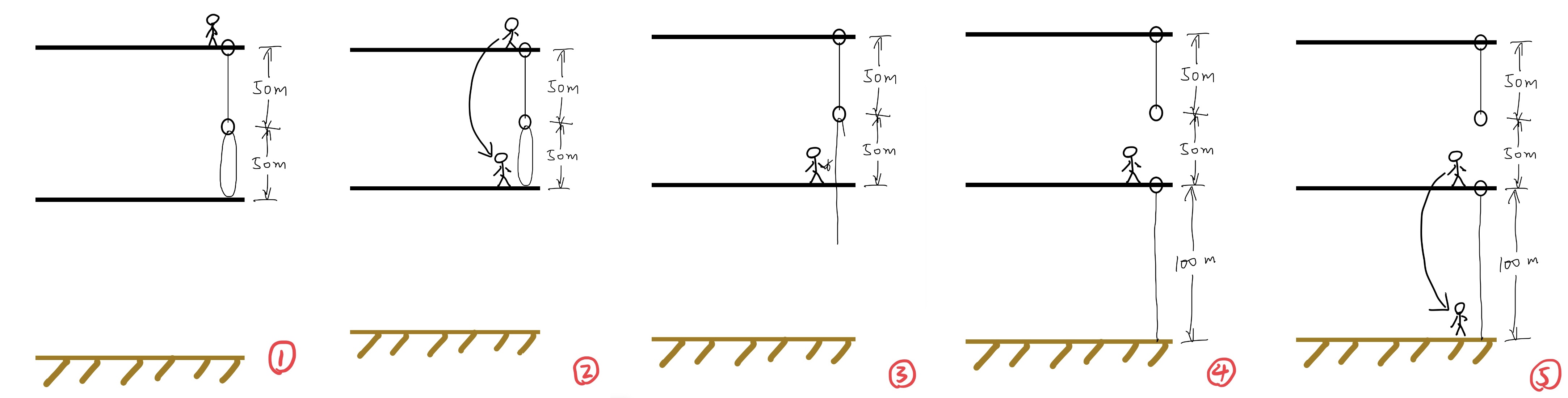
引入一个简单的问题作为铺垫。  假如你现在站在一栋高为 $200m$ 的楼上，人的大小忽略不计。 楼的 $100m$ 和 $200m$ 处分别突出一根无限长的钢管，人默认可以安全地站在上面。 你的手中有一把剪刀和一条长为 $150m$ 且极细的绳子，你可以打死结，不能打活结，且结的大小忽略不计。问你怎么安全下到地面。 解法： $150m$ 长的绳子不足以让我们直接下去，所以必然需要借助第二根钢管。于是我们考虑将绳子弄成这样子：  即将绳子剪成 $50m$ 和 $100m$ 两段，$50m$ 长的绳子的末端打一个小环，然后将 $100m$ 长的绳子穿入小环并首尾连接。这样就凑出了 $100m$ 的绳子。 把 $50m$ 绳子的另一端系在第一根钢管上，借助它下到第二根钢管，用剪刀剪断环，抽出 $100m$ 长的绳子，即可顺利下到地面。我们称这种方法为“环套”法。 以下是整个过程示意图。  注意：图中的圆圈代表绳两端系着的小环，实际大小忽略不计。 “环套法”中，我们把绳子分为两部分：环和链。其中环可以回收利用。 在接下来的题目场景中，我们默认只有“环套法”和“简化的环套法”两种方式可用。其中“简化的环套法”为环的长度为 $0$ 或链的长度为 $0$。 （感谢 huzheng20 提供的图 Orz）

在一栋楼上有 $n$ 个钢管，其中第 $i$ 个钢管高度为 $h_i$，权值为 $v_i$，你处在最高的某个钢管上，手中有一把剪刀和一条绳子，要求所经过的钢管权值必须组成单调**不减**序列。 某些钢管的高度可能相同，这意味着你在这个高度可以选择不同权值的钢管落脚。 你的绳子的初始长度必须为**正整数**，但你可以在使用环套法后回收得到一根非整数长度的绳子。 问最少需要多长的绳子才能下到地面。

第一行一个正整数 $n$，表示钢管个数。 接下来 $n$ 行，每行两个正整数 $h_i,v_i$，表示第 $i$ 个钢管的高度和权值。

一行一个正整数表示最少需要多长的绳子。

**本题开启捆绑测试**。 对于 $10\%$ 的数据，保证从高到低来看，钢管权值组成单调**不增**序列。 对于另外 $10\%$ 的数据，保证 $n\le 10^4$。 对于另外 $40\%$ 的数据，保证 $n\le 10^5$ 且不存在下标 $i,j$ 满足 $h_i=h_j$ 或 $v_i=v_j$。 对于所有数据，保证 $1\le n\le 5\times 10^5$，$1\le h,v\le 10^{18}$。