P9434 [NAPC-#1] Stage4 - Needle

>  > > — s10

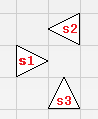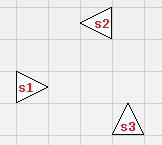
平面上有 $n$ 个**位置互不相同**的刺。刺有上下左右这 $4$ 种朝向。 定义一个【阴间刺】（其实就是削过的 sf 刺）为满足以下条件的有序刺**对** $(s_1,s_2,s_3)$： - $s_1$ 朝右，$s_2$ 朝左，$s_3$ 朝上。 - $x(s_1)y(s_1)>y(s_3)$。 - $x(s_2)-x(s_1)\leqslant d$。 其中 $x(s)$ 和 $y(s)$ 分别表示刺 $s$ 的横坐标和纵坐标；$d$ 为 kid 的宽度，在单组测试点中为常量。 坐标系 $x$ 轴正方向为从左到右，$y$ 轴正方向为从下到上。   上图是 $d\geqslant 2$ 时两个阴间刺的例子。~~虽然第二个刺型中 s3 对 kid 的跳跃没有影响/oh~~ 给出 $n$ 个刺的位置和朝向，请你告诉 kid 有多少（他跳不过去的）阴间刺。 显然朝下的刺在本题内是没有意义的。

**本题单测试点内有多组数据。** 第一行仅两个正整数 $T,id$ 表示测试数据的数量和测试点编号。特别地，样例的 $id=0$。 对于每组测试点，第一行输入两个正整数 $n,d$，表示刺的数量和 kid 的宽度，接下来 $n$ 行每行两个整数 $x,y$ 和一个字符 $c$ 表示一个刺的位置和朝向：`U` 代表朝上，`D` 代表朝下，`L` 代表朝左，`R` 代表朝右。

对于每组测试点，输出一行一个正整数表示阴间刺的数量。

### 【数据范围】 **本题采用捆绑测试。** $$ \def\r{\cr\hline} \def\arraystretch{1.5} \begin{array}{c|c|c|c|c} \textbf{Subtask} & id= & {\sum n\leqslant} & \textbf{Other Constraints} & \textbf{Score}\r \textsf1 & 1\sim 7 & 3\times10^4 & n\leqslant 30 & 10 \r \textsf2 & 31\sim45 & 10^4 & - & 25 \r \textsf3 & 8\sim10,16\sim17 & 10^5 & d=10^9 & 20 \r \textsf4 & 18\sim20 & 3\times10^5 & d=1 & 10 \r \textsf5 & 11\sim15,21\sim30 & 3\times10^5 & - & 35 \r \end{array} $$ 其中 $\sum n$ 表示单测试点内所有 $n$ 的总和。 对于 $100\%$ 的数据，$1\leqslant T\leqslant 2\times10^3$，$1\leqslant n\leqslant 3\times10^5$，$\sum n\leqslant 3\times10^5$，$1\leqslant d\leqslant 10^9$，$1\leqslant x,y\leqslant 10^9$，$(x,y)$ 互不相同，$c\in\{\texttt U, \texttt D, \texttt L, \texttt R \}$。 #### 【提示】 $\textbf{Sub}{\textsf2}$ 的 $O(n^2\log n)$ 做法和 $O(n^2)$ 做法都可以想想，可能都有些提示性……？qwq ### 【样例 #1-1 & #1-2 解释】 见【题目描述】中**两**幅图。 注意 #1-2 中 $d=1$，所以 kid 可以简单地钻缝过去，不算阴间。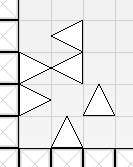 ### 【样例 #1-3 解释】  $4$ 个阴间刺分别为：$\Big((1,3),(2,4),(2,1)\Big),\Big((1,2),(2,4),(2,1)\Big),\Big((1,2),(2,3),(2,1)\Big),\Big((1,3),(2,4),(3,2)\Big)$ 即 $(5,6,1),(2,6,1),(2,4,1),(5,6,3)$（数字代表刺的下标：$i$ 代表第 $i$ 个刺）。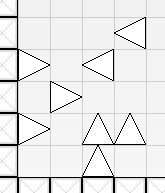 ### 【样例 #1-4 解释】  $6$ 个阴间刺分别为 $(2,1,7),(4,1,7),(4,3,6),(4,3,7),(4,3,8),(5,3,8)$。 【样例 #2】见附件，该样例除 $id=0$ 外满足 $\text{Subtask }\textsf1$ 的所有限制。