P9447 [ICPC 2021 WF] Spider Walk

夏洛特蜘蛛坐在她的蜘蛛网中心，蜘蛛网由一系列从中心延伸到外边界的丝线组成。夏洛特的网还有桥，每座桥连接两条相邻的丝线。桥的两个端点到蜘蛛网中心的距离总是相同。 当夏洛特在中心享用完深夜的盛宴后想要撤退到某个角落时，她会自动驾驶地走到边缘。为此，她选择一条起始丝线，并沿着它走，直到遇到这条丝线上的第一座桥。她会穿过桥到另一条丝线上，然后继续向外走，直到遇到另一座桥。然后她会穿过那座桥，并重复这个过程，直到当前丝线上没有更多的桥，然后她会走到当前丝线的末端。注意，夏洛特必须穿过她遇到的所有桥。图 I.1 展示了夏洛特可能走的一条路径。 夏洛特白天最喜欢睡觉的角落在丝线 $s$ 的末端。对于每个可能的起始丝线，她想知道为了最终到达 $s$，需要在原始网中添加的最少桥数。夏洛特可以在丝线的任何一点添加桥，只要添加的桥不接触任何其他桥。任何添加的桥的两个端点必须到蜘蛛网中心的距离相同，并且桥必须连接两条相邻的丝线。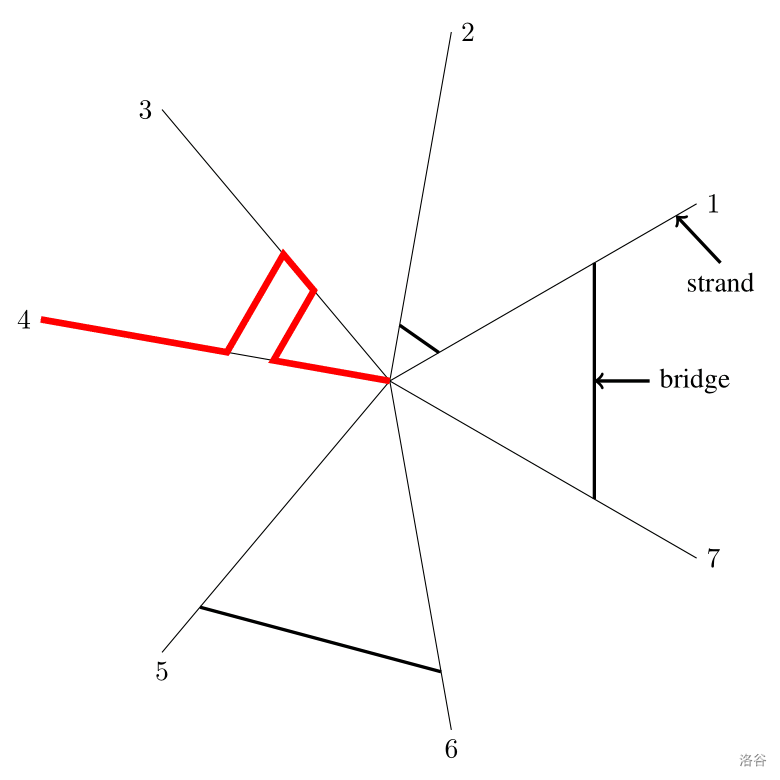  图 I.1：在示例输入 1 中从丝线 4 开始的路径。

输入的第一行包含三个整数 $n$、$m$ 和 $s$，其中 $n$ ($3 \leq n \leq 200000$) 是丝线的数量，$m$ ($0 \leq m \leq 500000$) 是桥的数量，$s$ ($1 \leq s \leq n$) 是夏洛特最喜欢的丝线。丝线按逆时针顺序从 $1$ 到 $n$ 标记。接下来的 $m$ 行中的每一行包含两个整数 $d$ 和 $t$ 描述一座桥，其中 $d$ ($1 \leq d \leq 10^9$) 是桥到蜘蛛网中心的距离，$t$ ($1 \leq t \leq n$) 是桥的第一条丝线的逆时针顺序。具体来说，如果 $1 \leq t < n$，则桥连接丝线 $t$ 和 $t+1$。如果 $t = n$，则桥连接丝线 $1$ 和 $n$。所有桥的距离 $d$ 都是不同的。

输出 $n$ 行，其中第 $i$ 行是夏洛特需要添加的最少桥数，以便在从丝线 $i$ 自动驾驶行走后最终到达丝线 $s$。

题面翻译由 ChatGPT-4o 提供。