P9456 [入门赛 #14] Three-View Projection (Hard Version)

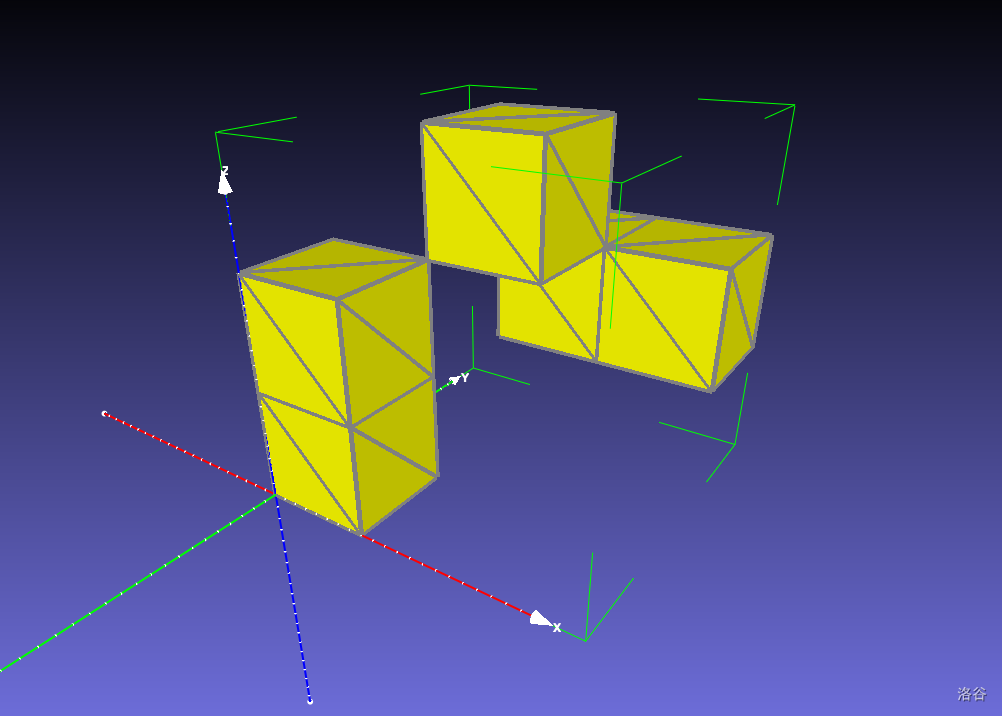
> 全文与 $x, y, z$ 轴/方向有关的内容均基于以下的 $x, y, z$ 轴、位置及观测方向。观测者站在如图所示的位置，正在向着 $y$ 轴（绿线）正方向（箭头方向）观测。 >  现在有一个长、宽、高（沿 $x, y, z$ 轴延展的长度）为 $n \text{ cm}, m \text{ cm}, k \text{ cm}$ 的长方体区域。我们将这片区域划分为 $n \times m \times k$ 个小格子。每个小格子中可以放置一个边长为 $1 \text{ cm}$ 的小正方体。 我们使用一个整数三元组 $(x, y, z)$ 来表示一个格子在空间中的位置，其代表从左往右数第 $x$ 个，从前往后数第 $y$ 个，从下往上第 $z$ 个格子。  例如，上图展示的 $3 \times 3 \times 3$ 区域中，按照观测者的位置，可以发现红蓝线（$x, z$ 轴）所在的面为前面，蓝绿线（$y, z$ 轴）所在的面为左面，红绿线（$x, y$ 轴）所在的面为下面，五个小正方体的位置分别为 $(1, 1, 1), (1, 1, 2), (2, 3, 2), (3, 3, 2), (2, 2, 3)$。 三视图是观测者从上面（从上往下）、左面（从左往右）、正面（从前往后）三个不同角度观察同一个空间几何体而画出的图形。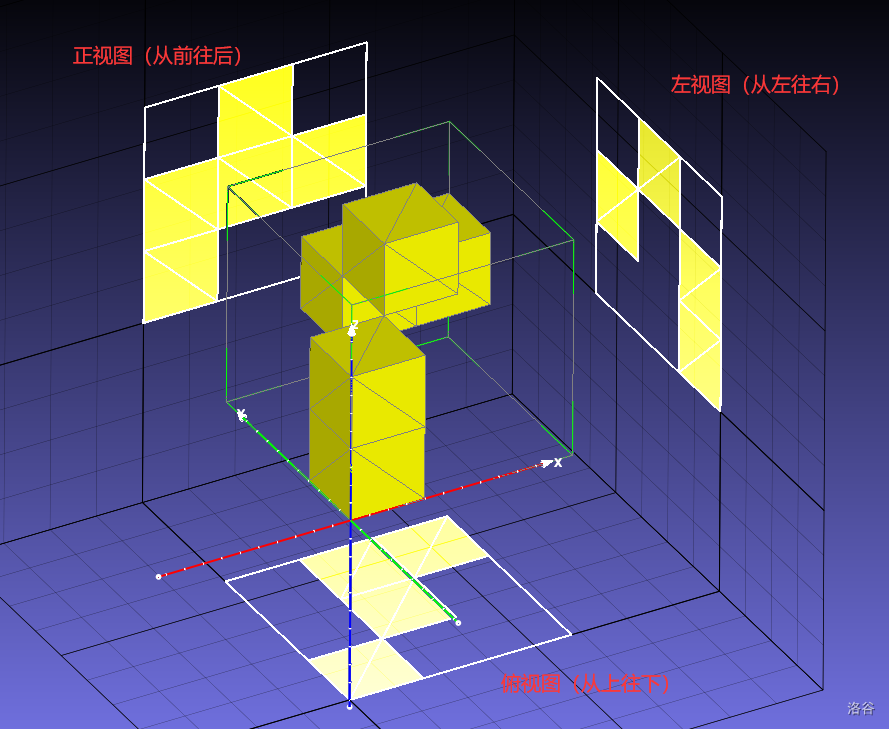   例如，以上是示例区域的三视图。 现在，给定一个区域及其中的正方体排布情况，请你帮助计算出这个区域的三视图。

输入共 $n \times k + 1$ 行。 第一行为三个整数 $n, m, k$，代表长方形区域的长、宽、高。 接下来 $n \times k$ 行，每行 $m$ 个整数。其中，将其每 $n$ 行分为一组，第 $x$ 组第 $y$ 行（即第 $(x - 1) \times n + y$ 行）第 $z$ 列的整数 $a _ {x, y, z}$ 代表 $(y, z, x)$ 处格子的情况，若 $a _ {x, y, z} = 1$，代表该格子有小正方体；否则，代表该格子没有小正方体。

输出共 $2k + m$ 行。 前 $k$ 行，每行 $n$ 个整数，代表**自上而下自左至右**正视图的情况。如果正视图中某个位置有填充，则输出 $1$，否则输出 $0$。同一行整数之间两两以一个空格隔开。 接下来 $k$ 行，每行 $m$ 个整数，代表**自上而下自后至前**左视图的情况。如果左视图中某个位置有填充，则输出 $1$，否则输出 $0$。同一行整数之间两两以一个空格隔开。 接下来 $m$ 行，每行 $n$ 个整数，代表**自后至前自左至右**俯视图的情况。如果俯视图中某个位置有填充，则输出 $1$，否则输出 $0$。同一行整数之间两两以一个空格隔开。 **以上方向均基于观测者初始站立位置及方向。如果对输出的顺序有疑惑，请参照样例辅助理解。**

### 样例 1 解释 样例 1 即为题目中的示例。  ### 数据规模与约定 对于 $100\%$ 的数据，保证 $1 \leq n, m, k \leq 200$，$0 \leq a _ {x, y, z} \leq 1$。