P9464 [EGOI 2023] Padel Prize Pursuit / 追梦笼式网球

Day 1 Problem B. 题面译自 [EGOI2023 ppp](https://egoi23.se/assets/tasks/day1/ppp.pdf)。 [](https://creativecommons.org/licenses/by-sa/3.0/)

有 $N$ 个编号为 $0$ 到 $N-1$ 的选手参加一场 $M$ 天的笼式网球锦标赛。每天恰好进行一次比赛。在锦标赛中共颁发 $M$ 块奖牌，每场比赛颁发一块新奖牌。在第 $i$ 天的比赛中（$0\le i\le M-1$），两名编号分别为 $x_i$ 和 $y_i$ 的选手参加。比赛中发生如下事件： - 选手 $x_i$ 打败选手 $y_i$。 - 一个新的奖牌授予给获胜者 $x_i$。 - 失败者所有现有的奖牌都授予给获胜者。 在第 $M$ 天（最后一场比赛结束后一天）举行颁奖典礼。在颁奖典礼上，所有奖牌被收集起来，并授予给持有该奖牌时间最长的选手。具体地，在第 $M$ 天，奖牌 $i$ 授予给持有奖牌 $i$ 最多个晚上的选手（不必须连续持有）。如果两个或更多选手持有一个奖牌同样多晚上，奖牌授予给其中编号最小的选手。 你的任务是求出颁奖典礼中，每位选手被授予多少奖牌。

第一行两个整数 $N,M$，表示选手数和比赛数。 接下来 $M$ 行，每行两个整数 $x_i,y_i$，表示第 $i$ 天的比赛中，选手 $x_i$ 打败选手 $y_i$。

一行 $N$ 个整数，第 $k$ 个整数表示颁奖典礼中，第 $k$ 位选手被授予的奖牌数。

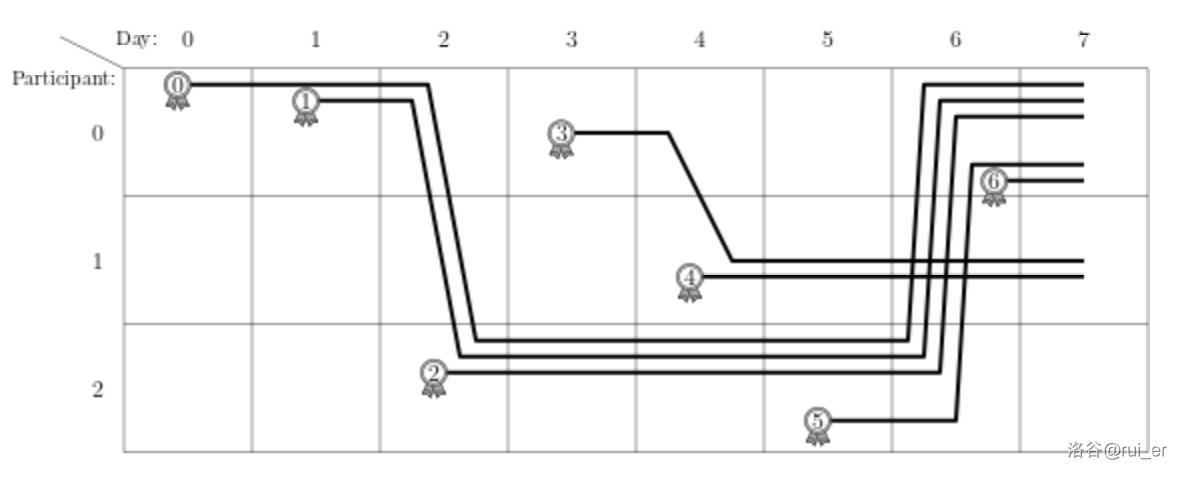
**样例 $1$ 解释** 下图展示了样例 $1$ 中锦标赛期间奖牌的归属。当选手 $1$ 在第三天被打败时，她的所有奖牌都被授予给选手 $2$。  --- **样例 $2$ 解释** 如下图。  在颁奖典礼中，选手 $0$ 被授予奖牌 $5$ 和 $6$，选手 $1$ 被授予奖牌 $3$ 和 $4$，选手 $2$ 被授予奖牌 $0,1,2$。 --- **数据范围** 对于全部数据，$2\le N\le 2\times 10^5$，$1\le M\le 2\times 10^5$，$0\le x_i,y_i\le N-1$ 且 $x_i\ne y_i$。 - 子任务一（$12$ 分）：$N=2$。 - 子任务二（$16$ 分）：$N,M\le 2\times 10^3$。 - 子任务三（$15$ 分）：第 $i$ 场比赛的获胜者参加了第 $i+1$ 场比赛，依赖子任务一。 - 子任务四（$20$ 分）：在第 $i$ 场比赛时，$x_i$ 有至少和 $y_i$ 一样多的奖牌。 - 子任务五（$22$ 分）：一旦一名选手被打败，她永远不会再次参赛。 - 子任务六（$15$ 分）：无特殊限制，依赖子任务二、三、四、五。