P9467 [EGOI 2023] Carnival General / 狂欢节总管

Day 2 Problem A. 题面译自 [EGOI2023 carnival](https://egoi23.se/assets/tasks/day2/carnival.pdf)。 [](https://creativecommons.org/licenses/by-sa/3.0/)

每四年，隆德的学生都会聚到一起并举办隆德狂欢节。几天之内，公园内会挤满帐篷，并举办各种各样的庆祝活动。负责组织这一切的人被称为狂欢节总管。 共有 $N$ 个狂欢节，每个狂欢节都有不同的总管。这些总管按时间顺序被编号为 $0$ 到 $N-1$。每个总管 $i$ 都给出了他们对于前任总管的评价，他们公布了总管 $0,1,\cdots,i-1$ 从好到坏的排名。 下一届隆德狂欢节将于 2026 年举办。在此期间，所有曾经的狂欢节总管聚在一起拍了张合照。然而，如果总管 $i$ 和 $j$（其中 $i < j$）最终紧挨着对方，且 $i$ 在 $j$ 给出的排名中**严格**位于后一半，那么就会很尴尬。 例如： - 如果总管 $4$ 给出的排名是 `3 2 1 0`，那么 $4$ 可以紧挨着 $3$ 或者 $2$ 站，但不能紧挨着 $1$ 或者 $0$。 - 如果总管 $5$ 给出的排名是 `4 3 2 1 0`，那么 $5$ 可以紧挨着 $4,3,2$ 站，但不能紧挨着 $1$ 或者 $0$。 下图为样例 $1$。其中，总管 $5$ 紧挨着总管 $2$ 和 $3$，且总管 $4$ 只紧挨着总管 $2$。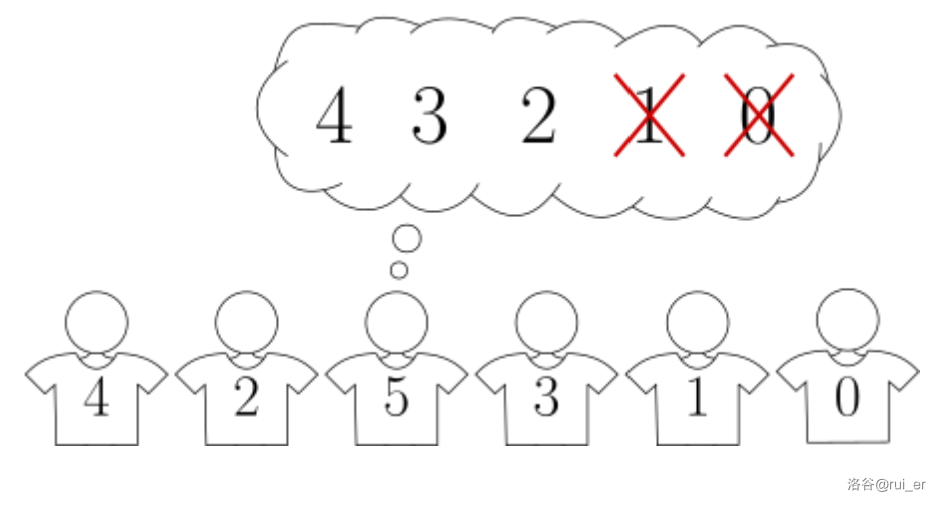  你已知所有总管给出的排名。你的任务是将所有总管 $0,1,\cdots,N-1$ 安排到一排，使得如果 $i$ 和 $j$ 紧挨着（其中 $i < j$），那么 $i$ **并非**严格位于 $j$ 给出排名的后一半。

第一行一个整数 $N$，表示总管总数。 接下来 $N-1$ 行包含所有排名。其中的第一行是总管 $1$ 给出的排名，第二行是总管 $2$ 给出的排名，以此类推直到总管 $N-1$。总管 $0$ 不在输入中，因为总管 $0$ 没有任何前任总管可供排名。 总管 $i$ 的排名是一个长度为 $i$ 的列表 $p_{i,0},p_{i,1},\cdots,p_{i,i-1}$，其中每个整数从 $0$ 到 $i-1$ 且恰好出现一次。具体地，根据总管 $i$ 的排名，$p_{i,0}$ 是最好的总管，$p_{i,i-1}$ 是最差的总管。

输出一列整数，一个整数 $0,1,\cdots,N-1$ 的排列，使得对于每对相邻整数，不存在一个在另一个排名的后一半。 可以证明一定有解。如果有多解，你可以输出任意一个。

**样例 $1$ 解释** 样例 $1$ 符合子任务一的要求。在样例中，总管 $2$ 和 $3$ 都不能紧挨着总管 $0$ 站，总管 $4$ 和 $5$ 都不能紧挨着总管 $0$ 和 $1$ 站。样例输出见上图。 --- **样例 $2$ 解释** 样例 $2$ 符合子任务二的要求。在样例中，总管 $2$ 不能紧挨着总管 $1$ 站，总管 $3$ 不能紧挨着总管 $2$ 站，总管 $4$ 不能紧挨着总管 $3$ 和 $2$ 站。 --- **样例 $3$ 解释** 样例 $3$ 符合子任务三的要求。在样例中，只有 $(1,3)$ 和 $(0,2)$ 两对总管不能彼此紧挨着站。因此，如果安排为 `3 0 1 2`，并不会有冲突。另一种可能的答案是 `0 1 2 3`。 --- **数据范围** 对于全部数据，$2\le N\le 10^3$，$0\le p_{i,0},p_{i,1},\cdots,p_{i,i-1}\le i-1$。 - 子任务一（$11$ 分）：总管 $i$ 给出的排名为 $i-1,i-2,\cdots,0$。 - 子任务二（$23$ 分）：总管 $i$ 给出的排名为 $0,1,\cdots,i-1$。 - 子任务三（$29$ 分）：$N\le 8$。 - 子任务四（$37$ 分）：无特殊限制。