P9469 [EGOI 2023] Sopsug / 垃圾处理

Day 2 Problem C. 题面译自 [EGOI2023 sopsug](https://egoi23.se/assets/tasks/day2/sopsug.pdf)。 [](https://creativecommons.org/licenses/by-sa/3.0/)

砾石堆是隆德郊区的一处未建成的居民区。目前，所有必要的基础设施正在建设中，包括其中最重要的：垃圾处理。与瑞典许多地区一样，将使用一个自动真空收集系统收集垃圾。其原理是使用气压将垃圾通过管道在地下运输。 砾石堆中有 $N$ 座建筑，编号从 $0$ 到 $N-1$。你的任务是用管道连接几对建筑。如果你在建筑 $u$ 和 $v$ 之间连接一条管道，$u$ 将会把所有垃圾运送到 $v$（但不能反向运输）。你的目标是建立一个由 $N-1$ 个管道组成的网络，使得所有垃圾最终都进入一座建筑。换句话说，你希望整个网络构成一棵有根树，所有边都指向树根。 然而，建筑物间已经建设了 $M$ 条管道。这些管道必须被包含在你的网络中。这些管道是有方向的，只能向一个方向运输。 此外，有 $K$ 对建筑物间无法建设管道。这些建筑物对是有序的，因此如果无法从 $u$ 到 $v$ 建设管道，也有可能从 $v$ 到 $u$ 可以建设管道。

第一行三个整数 $N,M,K$。 接下来 $M$ 行，每行两个不相等的整数 $a_i,b_i$，表示已经存在一条从 $a_i$ 到 $b_i$ 的管道。 接下来 $K$ 行，每行两个不相等的整数 $c_i,d_i$，表示无法从 $c_i$ 到 $d_i$ 建设管道。 所有 $M+K$ 对有序数对是互不相同的。注意 $(u,v)$ 和 $(v,u)$ 是不同的两对数。

如果无解，输出 `NO`。 否则，输出 $N-1$ 行，每行两个整数 $u_i,v_i$，表示有一条从 $u_i$ 到 $v_i$ 的管道。你可以以任意顺序输出这些管道。如果有多解，你可以输出任意一个。请记住所有 $M$ 条已经存在的管道必须包含在答案中。

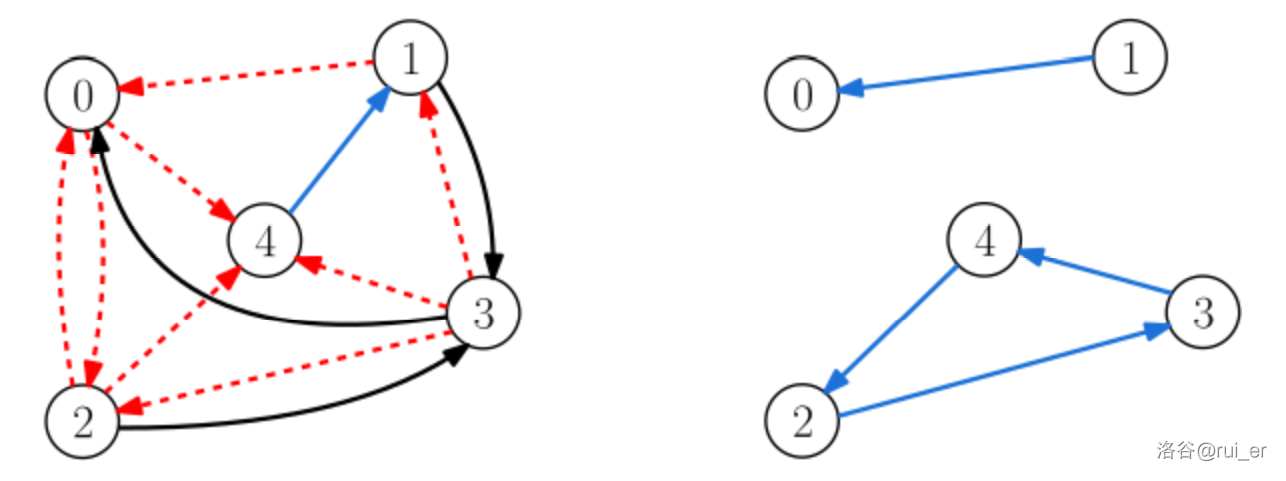
**样例 $1,2$ 解释** 下图展示了前两组样例。蓝色边表示已经存在的管道，红色虚线边表示无法建造的管道。 左图展示了样例 $1$ 和样例输出的方案，黑色边表示新建造的管道。在这个网络中，所有垃圾将被收集在建筑 $0$。这不是唯一解；例如，从 $1$ 到 $3$ 的管道可以被从 $0$ 到 $1$ 的管道代替，此时依然是合法解。 对于样例 $2$，根据右图可以发现，由于环 $(2,3,4)$ 的存在，问题无解。  --- **数据范围** 对于全部数据，$2\le N\le 3\times 10^5$，$0\le M\le 3\times 10^5$，$0\le K\le 3\times 10^5$，$0\le a_i,b_i\le N-1$，$0\le c_i,d_i\le N-1$。 - 子任务一（$12$ 分）：$M=0$，$K=1$。 - 子任务二（$10$ 分）：$M=0$，$K=2$。 - 子任务三（$19$ 分）：$K=0$。 - 子任务四（$13$ 分）：$N\le 100$。 - 子任务五（$17$ 分）：保证存在解法使得 $0$ 为根。 - 子任务六（$11$ 分）：$M=0$。 - 子任务七（$18$ 分）：无特殊限制。