P9470 [EGOI 2023] Guessing Game / 猜猜看（通信题无法评测）

Day 2 Problem D. 题面译自 [EGOI2023 guessinggame](https://egoi23.se/assets/tasks/day2/guessinggame.pdf)。 [](https://creativecommons.org/licenses/by-sa/3.0/)

**本题是一道通信题。** 在隆德老城中，有一个街道依次有 $N$ 座房子，编号从 $0$ 到 $N-1$。埃玛住在其中一间房子中，她的朋友安娜和贝蒂尔希望找出到底是哪间。埃玛决定跟他们玩一个游戏，而不直接告诉他们她住在哪里。在游戏开始前，安娜和贝蒂尔只知道街道上的房子数。此时，安娜和贝蒂尔可以选择一个正整数 $K$ 并确定策略。之后禁止一切交流。 游戏本身分为两个阶段。在第一阶段，埃玛选择一个访问房子的顺序，使得她的房子最后被访问。然后，她带领安娜按照这个顺序依次前往房子，并不提前告知安娜这个顺序。对于每个不是埃玛房子的房子，安娜被允许用粉笔在前门上写下一个 $1$ 到 $K$ 的整数。对于她们最后访问的房子，也就是埃玛的房子，埃玛自己在门上写下一个 $1$ 到 $K$ 的整数。 在第二阶段，贝蒂尔在街道上依次经过编号为 $0$ 到 $N-1$ 的房子，并读到安娜和埃玛在门上写下的数字。然后，他希望猜出埃玛的房子。他有两次机会猜出答案，如果他成功猜出答案，他和安娜就赢了游戏。否则，埃玛赢了游戏。 你能给出一种策略，使得安娜和贝蒂尔必胜吗？你的策略将被根据 $K$ 的值评分（越小越好）。

无

本题是一道通信题，意味着你的程序会被运行多次。第一次运行时，它会执行安娜的策略。之后，它会执行贝蒂尔的策略。 输入的第一行包括两个整数 $P$ 和 $N$，其中 $P$ 为 $1$ 或 $2$（第一阶段或第二阶段），$N$ 表示房子数。**除了样例输入（不被用于计分），$N$ 永远为 $10^5$。** 接下来的输入根据阶段决定： **第一阶段** 你的程序首先输出整数 $K$ 并换行（$1\le K\le 10^6$）。然后，重复 $N-1$ 次，读入一行一个整数 $i$（$0\le i < N$），并输出一行一个整数 $A_i$（$1\le A_i\le K$），其中 $A_i$ 是安娜在房子 $i$ 的门上写的数字。每一个整数 $i$（除了埃玛的房子）会出现恰好一次，顺序由交互库决定。 **第二阶段** 你的程序应当读入一行 $N$ 个整数 $A_0,A_1,\cdots,A_{N-1}$，其中 $A_i$ 是写在房子 $i$ 的门上的数字。 然后，输出一行两个整数 $s_1$ 和 $s_2$（$0\le s_i < N$），表示猜测的房子编号。$s_1$ 和 $s_2$ 被允许相等。 **实现细节** 注意当你的程序运行第二阶段时，程序被重新启动。这意味着两个阶段之间，你不能在变量中保存信息。 请确保在输出每行后刷新输出流，否则你的程序可能被判定为 TLE。在 Python 中，`print()` 自动刷新输出流。在 C++ 中，`cout

**样例解释** 样例测试点不被计入总分中，你的程序不必支持样例测试点。 假设我们有 $N=4$ 且埃玛住在房子 $1$。令 $A$ 为每个房子上写的数的列表。初始时，$A=[0,0,0,0]$，其中 $0$ 表示对应房子上还没有被写数。 在第一次运行中： 已知 $N=4$。你的程序回答 $K=3$。 $A_2$ 被问及。你的程序回答 $3$。$A$ 现在是 $[0,0,3,0]$。 $A_0$ 被问及。你的程序回答 $1$。$A$ 现在是 $[1,0,3,0]$。 $A_3$ 被问及。你的程序回答 $2$。$A$ 现在是 $[1,0,3,2]$。 最终，交互库设置 $A_1=2$，因此 $A=[1,2,3,2]$。这标志着第一阶段的结束。 在第二阶段中，你的程序已知列表 `1 2 3 2`。 你的程序回答 `1 3`。 由于其中一次猜测是正确的（$1$），安娜和贝蒂尔赢得了游戏。 --- **评分方式** 你的程序会被测试于一定数量的测试点。如果你的程序在*任何*一个测试点失败（例如：给出错误答案（WA）、程序崩了（RE）、超出时间限制（TLE）等），你会得到 $0$ 分和适当的评测结果。 如果你的程序在*所有*测试点都成功找到了埃玛的房子，你会得到 AC（**译者注：在洛谷，非满分即为 WA**），分数按照下表计算。令 $K_{\max}$ 是所有测试点中最大的 $K$ 值。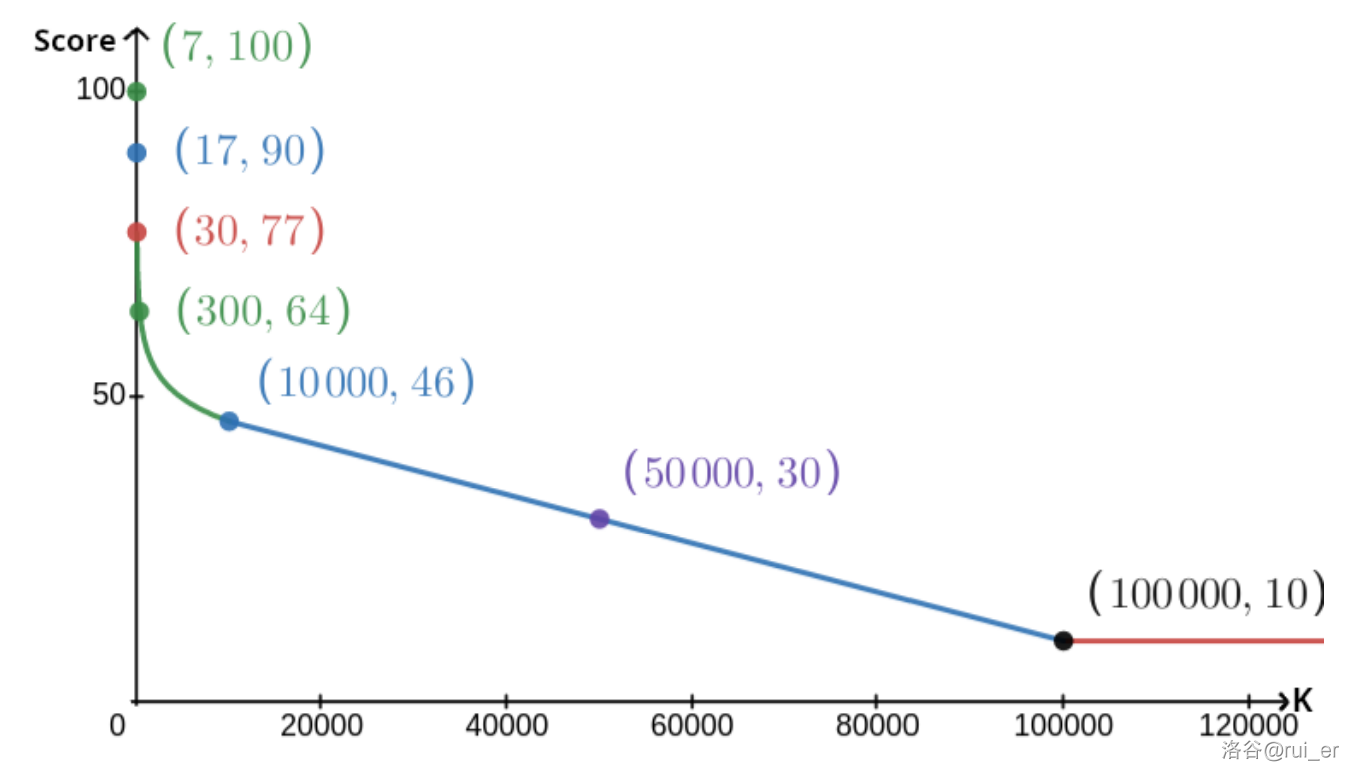根据 $K_{\max}$： ||分数| |:-|:-| |$K_{\max} > 99998$|$10$| |$10000 < K_{\max}\le 99998$|$10+\lfloor40(1-\frac{K_{\max}}{10^5})\rfloor$| |$30 < K_{\max}\le 10000$|$46+\lfloor\frac{31(4-\lg K_{\max})}{4-\lg 30}\rfloor$| |$7 < K_{\max}\le 30$|$107-K_{\max}$| |$K_{\max}\le 7$|$100$| 计分函数图象如下：  样例测试点不被计入总分中，你的程序不必支持样例测试点。