P9545 [湖北省选模拟 2023] 环山危路 / road

R 国有 $n$ 座城市，编号从 $1$ 到 $n$。这些城市两两之间都有道路连接，形成一个图的结构。不过，这些路修得很烂，每条路都有一个固定的方向，车只能按照这个方向行驶；路还是一次性的，也就是说最多只能过一辆车。 现在 R 国正在制定防灾减灾预案。你需要帮助 R 国计算，如果 $t_i$ 号城市发生了灾难，并且 $s_{i,1},s_{i,2},\dots,s_{i,k_i}$ 这些城市有充足的救灾物资（可以认为它们都拥有可以装无数辆车的物资），那么最多能从这些城市运送几车物资到达 $t_i$。车只能走城间的那些一次性道路，不过车在到达 $t_i$ 之前是可以经过多个城市和多条道路中转的。

输入共 $n+m +1$ 行。 第一行两个正整数 $n,m$，表示城市个数和询问次数。 第二行到第 $n+1$ 行，每行一个长为 $n$ 的 $01$ 字符串，第 $i+1$ 行第 $j$ 列表示是否有从 $i$ 通向 $j$ 的道路（$1$ 表示有，$0$ 表示无）。 接下来 $m$ 行，每行第一个正整数为 $t_i$，第二个正整数为 $k_i$，接着 $k_i$ 个正整数 $s_{i,1},s_{i,2},\dots,s_{i,k_i}$。保证 $s_{i,1},s_{i,2},\dots,s_{i,k_i}$ 中没有重复的数且没有 $t_i$。

输出 $m$ 行，每行一个非负整数，表示第 $i$ 次询问的答案。

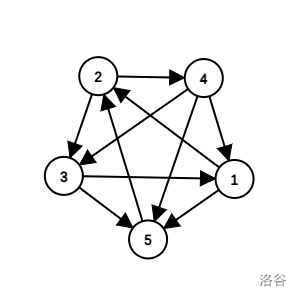
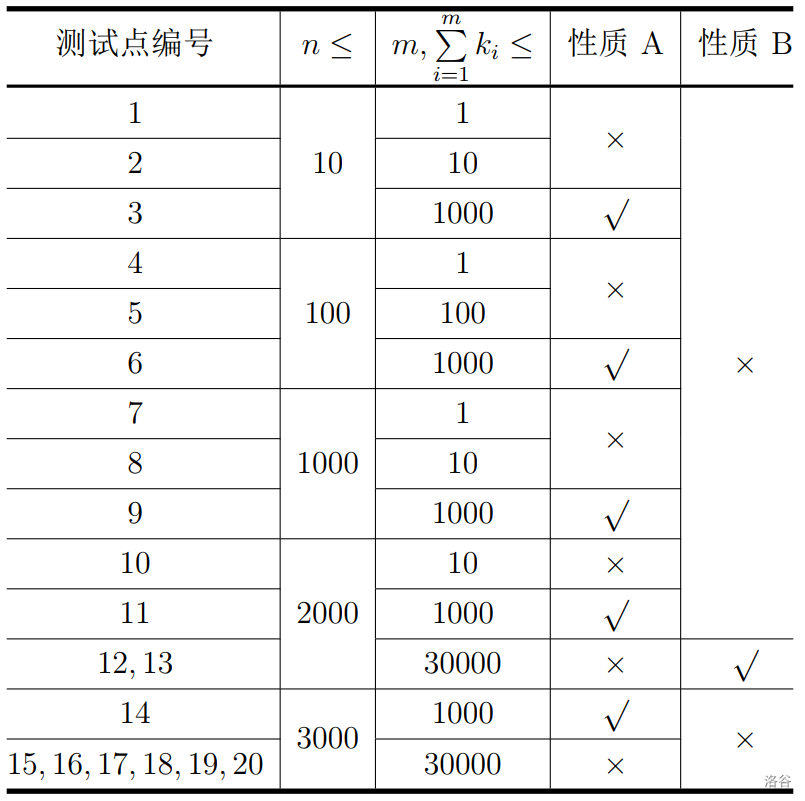
### 样例 1 解释 城市间的路如下图所示：  这是答案对应的一种可能的方案： 第一次询问中，一辆车走 $1 \rightarrow 2$，另一辆走 $4 \rightarrow 1 \rightarrow 5 \rightarrow 2$； 第二次询问中，一辆车走 $1 \rightarrow 5$，一辆走 $1 \rightarrow 2 \rightarrow 3 \rightarrow5$，还有一辆走 $4 \rightarrow 5$。 ### 子任务 对于所有测试数据，保证 $1 \le n \le 3000$，$1 \le m,\sum\limits_{i=1}^mk_i \le 30000$。  特殊性质 A：保证所有询问的 $t_i$ 相等。 特殊性质 B：保证 $u$ 与 $v$ 之间的路从 $\min(u,v)$ 通向 $\max(u,v)$。