P9547 [湖北省选模拟 2023] 路环群山 / mountain

某二维世界中有一个山地，山体可以用一个函数 $f(x)$ 描述，其表示横坐标 $x$ 的位置海拔高度为 $h=f(x)$。这个世界里有 $n+m$ 只羊，其中有 $n$ 只山羊和 $m$ 只绵羊。我们知道第 $i$ 只山羊所在的横坐标是 $p_i$，第 $j$ 只绵羊所在的横坐标是 $q_j$，但不知道它们所在的高度。不过，我们知道山羊们所在的位置海拔集中在一个较高的范围，而绵羊们所在的位置海拔集中在一个较矮的范围。你需要根据山羊和绵羊的分布情况猜测山体形态 $f(x)$，使得山羊高度的方差和绵羊高度的方差都尽可能小，同时山羊高度尽可能高于绵羊高度。 形式化地，令 $$ \bar{u}=\frac{1}{n}\sum_{i=1}^n f(p_i) $$ $$ \bar{v}=\frac{1}{m}\sum_{j=1}^m f(q_i) $$ 表示山羊、绵羊分别的平均高度，你的目标就是构造函数 $f$，最小化代价 $$ \operatorname{cost}(f)=\frac{1}{\bar{u}-\bar{v}}\sqrt{\left[\sum_{i=1}^n (f(p_i)-\bar{u})^2\right]+\left[\sum_{j=1}^m (f(q_j)-\bar{v})^2\right]} $$ 当然，**你还需要保证 $\bar u > \bar v + 10^{-9}$**。 方便起见，你需要使用傅里叶级数描述 $f$。即给定 $k$，你需要求出最优的形如 $f(x)=\sum_{i=1}^k a_i\cos(ix)+b_i\sin(ix)$ 的函数 $f$，并输出 $a_i,b_i$ 表示答案。**请你保证 $10^{-9}\le \max_{i=1}^k\{|a_i|,|b_i|\} \le 10^9$**。**数据保证存在满足上述限制的最优解。** 本题开启 Special Judge。给定容错度 $\epsilon=10^{-E}$。当你给出的函数 $f$ 与答案给出的函数 $f^*$ 满足 $\operatorname{cost}(f)

输入共三行。 第一行三个整数 $n,m,k,E$； 第二行 $n$ 个整数，第 $i$ 个数为 $p_i$； 第三行 $m$ 个整数，第 $j$ 个数为 $q_j$。

输出 $k$ 行，每行两个浮点数 $a_i,b_i$。

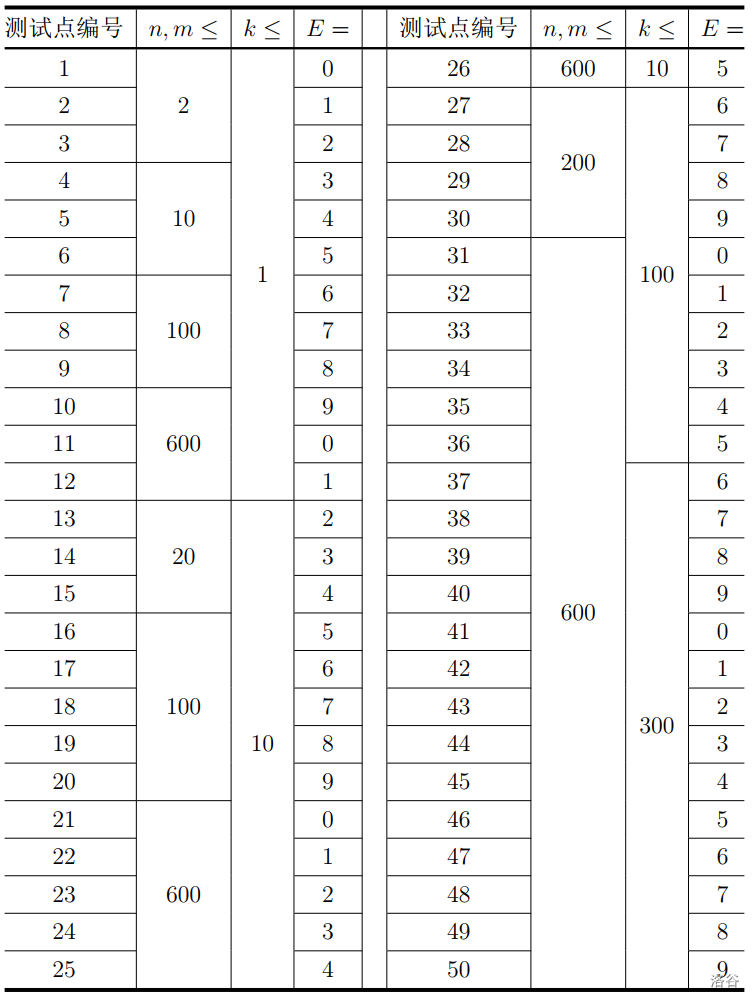
### 样例 1 解释 观察到 $\cos(10838702)=\cos(-10838702)\approx 1 =\cos(0)$，$\cos(1)=\cos(-1)\approx 0.5403023$。即当 $f(x)=\cos(x)$ 时，所有山羊几乎均位于同一海拔、所有绵羊均位于同一海拔、山羊所在位置均高于绵羊所在位置。此时 $\operatorname{cost}(f) \approx 0$ 取得最优解。 值得注意的是，对于任何非零数 $r$，函数 $f(x)=r\cos(x)$ 均可视为最优解。 ### 样例 2 解释 最优函数（之一）约为 $f(x)=0.6648289523\cos(x)-0.1433645347\sin(x)+0.6172866488\cos(2x)+1.3647253547\sin(2x)$，其代价约为 $3.908439063011$。 ### 子任务 对于所有测试数据，保证 $1 \le n,m \le 600$，$1 \le k \le \min\{\dfrac{n+m}{4},300\}$，$0 \le E \le 9$，$0\le |p_i|,|q_i| \le 10^9$。 **保证每个测试数据中，$p_i$ 和 $q_j$ 均在该测试点数据范围内以及问题有解的条件下均匀随机生成。**