P9563 [SDCPC 2023] Be Careful 2
题目描述
小青鱼有一个位于二维平面上的,大小为 $n \times m$ 的矩形。矩形的右上角位于 $(n, m)$,而左下角位于 $(0, 0)$。矩形内部有 $k$ 个禁止点,第 $i$ 个禁止点位于 $(x_i, y_i)$。
小青鱼想在矩形里画一个正方形。但由于小青鱼不喜欢禁止点,因此正方形的内部不能有任何禁止点。更正式地,小青鱼可以画一个左下角位于 $(x, y)$ 且边长为 $d$ 的正方形,当且仅当:
- $x$ 和 $y$ 都是非负整数,$d$ 是一个正整数。
- $0 \leq x < x+d \leq n$。
- $0 \leq y < y+d \leq m$。
- 每个 $1 \leq i \leq k$ 都 **不能** 满足以下条件:
- $x < x_i < x+d$ 且 $y < y_i < y+d$。
请计算小青鱼可以画的正方形的总面积。由于答案可能很大,请将答案对 $998244353$ 取模后输出。
输入格式
每个测试文件仅有一组测试数据。
第一行输入三个整数 $n$,$m$ 和 $k$($2 \leq n,m \leq 10^9$,$1 \leq k \leq 5 \times 10^3$),表示矩形的大小和禁止点的数量。
对于接下来 $k$ 行,第 $i$ 行输入两个整数 $x_i$ 和 $y_i$($0 < x_i < n$,$0 < y_i < m$)表示第 $i$ 个禁止点的位置。保证所有禁止点互不相同。
输出格式
输出一行一个整数,代表对 $998244353$ 取模后的答案。
**【样例解释】**
对于第一组样例数据,小青鱼有 $12$ 种方式画一个正方形,如下图所示。
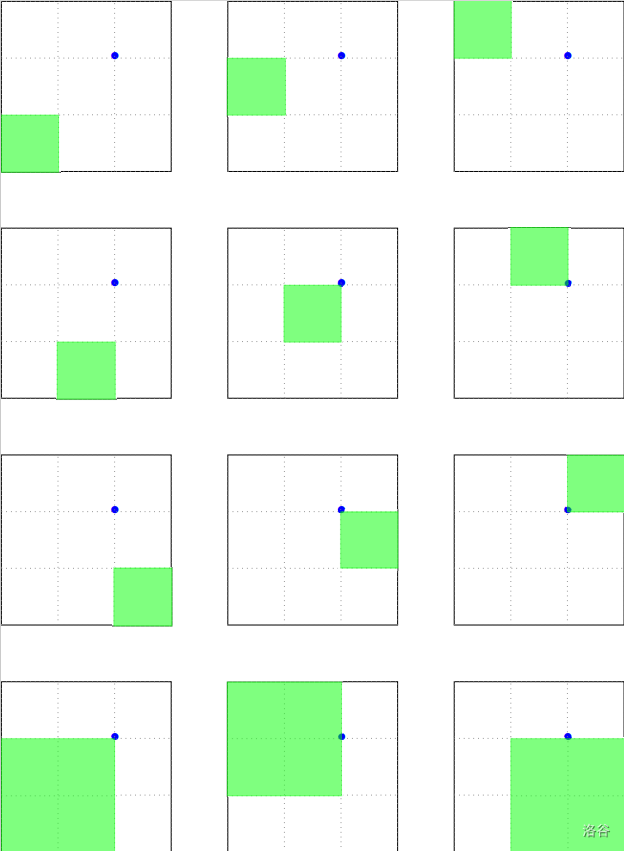
共有 $9$ 个边长为 $1$ 的正方形和 $3$ 个边长为 $2$ 的正方形。因此答案为 $9 \times 1^2 + 3 \times 2^2 = 21$。
以下画正方形的方式是不合法的,因为正方形内有一个禁止点。
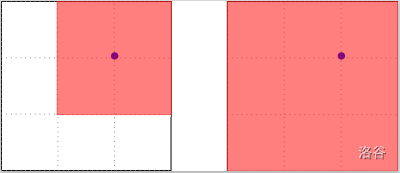
说明/提示
For the first sample test case, Little Cyan Fish has $12$ ways to draw a square, illustrated as follows.

There are $9$ squares of side length $1$ and $3$ squares of side length $2$. So the answer is $9 \times 1^2 + 3 \times 2^2 = 21$.
Note that the following plans are invalid since there's a banned point in the square.
