P9563 [SDCPC 2023] Be Careful 2

# 警告：滥用本题评测将被封禁。

Little Cyan Fish has an $n \times m$ rectangle located in a plane. The top-right corner of the rectangle is at $(n, m)$, while the bottom-left corner is at $(0, 0)$. There are $k$ banned points inside the rectangle. The $i$-th banned point is located at $(x_i, y_i)$. Little Cyan Fish would like to draw a square inside the rectangle. However, he dislikes all the banned points, so there cannot be any banned points inside his square. Formally, Little Cyan Fish can draw a square with the bottom-left corner at $(x, y)$ and a side length $d$ if and only if: - Both $x$ and $y$ are non-negative integers while $d$ is a positive integer. - $0 \leq x < x+d \leq n$. - $0 \leq y < y+d \leq m$. - For each $1 \leq i \leq k$, the following condition must **NOT** be met: - $x < x_i < x+d$ and $y < y_i < y+d$. Please calculate the sum of the areas of all the squares that Little Cyan Fish can possibly draw. Since the answer could be huge, you need to output it modulo $998244353$.

The is only one test case in each test file. The first line of the input contains three integers $n$, $m$ and $k$ ($2 \leq n,m \leq 10^9$, $1 \leq k \leq 5 \times 10^3$) indicating the size of the rectangle and the number of banned points. For the following $k$ lines, the $i$-th line contains two integers $x_i$ and $y_i$ ($0 < x_i < n$, $0 < y_i < m$) indicating the position of the $i$-th banned point. It is guaranteed that all the banned points are distinct.

Output one line containing one integer indicating the answer modulo $998244353$.

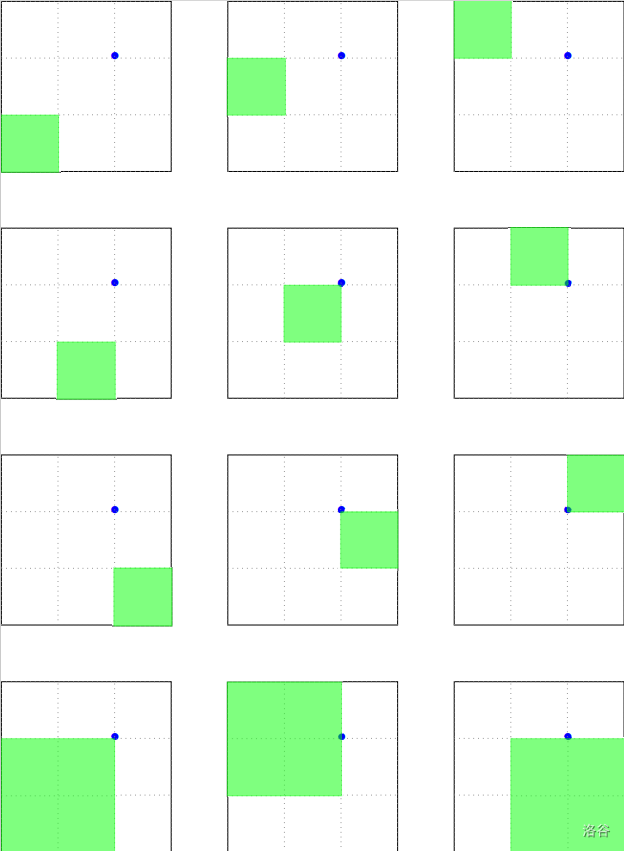
For the first sample test case, Little Cyan Fish has $12$ ways to draw a square, illustrated as follows.  There are $9$ squares of side length $1$ and $3$ squares of side length $2$. So the answer is $9 \times 1^2 + 3 \times 2^2 = 21$. Note that the following plans are invalid since there's a banned point in the square.