P9565 [SDCPC 2023] Not Another Path Query Problem

> What age is it that you are still solving traditional path query problems?

After reading the paper *Distributed Exact Shortest Paths in Sublinear Time*, you have learned how to solve the distributed single-source shortest paths problem in $\mathcal{O}(D^{1/3} \cdot (n \log n)^{2/3})$. To give your knowledge good practice, Little Cyan Fish prepared the following practice task for you. Little Cyan Fish has a graph consisting of $n$ vertices and $m$ bidirectional edges. The vertices are numbered from $1$ to $n$. The $i$-th edge connects vertex $u_i$ to vertex $v_i$ and is assigned a weight $w_i$. For any path in the graph between two vertices $u$ and $v$, let's define the value of the path as the bitwise AND of the weights of all the edges in the path. As a fan of high-value paths, Little Cyan Fish has set a constant threshold $V$. Little Cyan Fish loves a path if and only if its value is at least $V$. Little Cyan Fish will now ask you $q$ queries, where the $i$-th query can be represented as a pair of integers $(u_i, v_i)$. For each query, your task is to determine if there exists a path from vertex $u_i$ to vertex $v_i$ that Little Cyan Fish would love it.

There is only one test case in each test file. The first line contains four integers $n$, $m$, $q$ and $V$ ($1 \le n \le 10^5$, $0 \le m \le 5 \times 10^5$, $1 \leq q \leq 5 \times 10^5$, $0 \leq V < 2^{60}$) indicating the number of vertices, the number of edges, the number of queries and the constant threshold. For the following $m$ lines, the $i$-th line contains three integers $u_i$, $v_i$ and $w_i$ ($1 \le u_i,v_i \le n$, $u_i \ne v_i$, $0 \leq w_i < 2^{60}$), indicating a bidirectional edge between vertex $u_i$ and vertex $v_i$ with the weight $w_i$. There might be multiple edges connecting the same pair of vertices. For the following $q$ lines, the $i$-th line contains two integers $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq n$, $u_i \ne v_i$), indicating a query.

For each query output one line. If there exists a path whose value is at least $V$ between vertex $u_i$ and $v_i$ output `Yes`, otherwise output `No`.

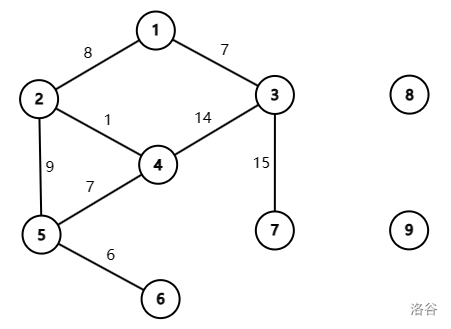
We now use $\&$ to represent the bitwise AND operation. The first sample test case is shown as follows.  - For the first query, a valid path is $1 \to 3 \to 4 \to 5 \to 6$, whose value is $7 \,\&\, 14 \,\&\, 7 \,\&\, 6 = 6 \ge 5$. - For the third query, a valid path is $7 \to 3 \to 4 \to 5 \to 6$, whose value is $15 \,\&\, 14 \,\&\, 7 \,\&\, 6 = 6 \ge 5$. - For the fourth query, as there is no path between vertex $1$ and $8$, the answer is `No`. For the only query of the second sample test case, we can consider the path consisting of the $2$-nd and the $4$-th edge. Its value is $5 \,\&\, 6 = 4 \ge 4$.