P9567 [SDCPC 2023] Puzzle: Sashigane
题目描述
给定一个 $n$ 行 $n$ 列的网格,网格中包含恰好一个黑色方格,其余方格均为白色。令 $(i, j)$ 表示位于第 $i$ 行第 $j$ 列的格子,这个黑色方格位于 $(b_i, b_j)$。
您需要用若干 L 形覆盖所有白色格子,使得每个白色格子都恰好被一个 L 形所覆盖,同时唯一的黑色方格不能被任何 L 形覆盖。L 形不能超过网格的边界。
更正式地,网格中的一个 L 形由四个整数 $(r, c, h, w)$ 唯一确定,其中 $(r, c)$ 确定了 L 形的转折点,$h$ 和 $w$ 确定了 L 形两臂的方向和长度。四个整数满足 $1 \le r, c \le n$,$1 \le r + h \le n$,$1 \le c + w \le n$,$h \ne 0$,$w \ne 0$。
- 若 $h < 0$,则所有满足 $r + h \le i \le r$ 的格子 $(i, c)$ 均属于该 L 形;否则若 $h > 0$,则所有满足 $r \le i \le r + h$ 的格子 $(i, c)$ 均属于该 L 形。
- 若 $w < 0$,则所有满足 $c + w \le j \le c$ 的格子 $(r, j)$ 均属于该 L 形;否则若 $w > 0$,则所有满足 $c \le j \le c + w$ 的格子 $(r, j)$ 均属于该 L 形。
下图展示了几种 L 形。
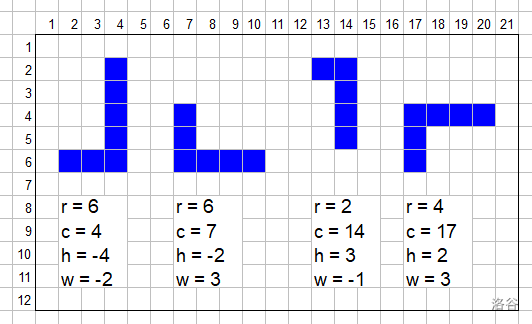
输入格式
每个测试文件仅有一组测试数据。
第一行输入三个整数 $n$,$b_i$,$b_j$($1 \le n \le 10^3$,$1 \le b_i, b_j \le n$)表示网格的大小以及黑色格子的位置。
输出格式
如果存在符合要求的覆盖方案,首先输出一行 `Yes`,接下来在第二行输出一个整数 $k$($0 \leq k \leq \frac{n^2-1}{3}$)表示覆盖白色格子的 L 形数量。接下来输出 $k$ 行,第 $i$ 行输出四个由单个空格分隔的整数 $r_i$,$c_i$,$h_i$ 和 $w_i$,表示第 $i$ 个 L 形由 $(r_i, c_i, h_i, w_i)$ 唯一确定。如果有多种合法答案,您可以输出任意一种。
如果不存在符合要求的覆盖方案,仅需要输出一行 `No`。
**【样例解释】**
第一组样例数据展示如下。
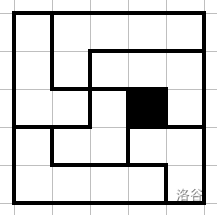
说明/提示
We illustrate the first sample test case as follows.
