P9568 [SDCPC 2023] Computational Geometry
题目描述
给定一个有 $n$ 个顶点的凸多边形 $P$,您需要选择 $P$ 的三个顶点,按逆时针顺序记为 $a$,$b$ 和 $c$。要求在 $b$ 沿逆时针方向到 $c$ 之间恰有 $k$ 条边(也就是说,$a$ 不是这 $k$ 条边的端点)。
考虑用线段 $ab$ 和 $ac$ 将 $P$ 割开。将由线段 $ab$,$ac$,以及 $b$ 和 $c$ 之间的 $k$ 条边围成的 $(k + 2)$ 边形记作 $Q$。
求 $Q$ 可能的最大面积。
注意,$ab$ 和 $ac$ 可以与 $P$ 的边重合。
输入格式
有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数。对于每组测试数据:
第一行输入两个整数 $n$ 和 $k$($3 \le n \le 10^5$,$1 \le k \le n-2$),表示凸多边形 $P$ 的顶点数和 $b$ 沿逆时针方向到 $c$ 之间的边数。
对于接下来的 $n$ 行,第 $i$ 行输入两个整数 $x_i$ 和 $y_i$($-10^9 \le x_i, y_i \le 10^9$),表示凸多边形 $P$ 第 $i$ 个顶点的 $x$ 坐标和 $y$ 坐标。顶点按逆时针顺序给出。保证凸多边形的面积为正,且没有顶点会重合。可能存在三个顶点位于同一条直线上的情况。
保证所有数据 $n$ 之和不超过 $10^5$。
输出格式
每组数据输出一行一个实数表示 $Q$ 的最大可能面积。只要您的答案的相对误差或绝对误差小于$10^{-9}$ 即视为正确。
**【样例解释】**
对于第一组样例数据,$Q$ 就是整个三角形,面积为 $0.5$.
第二和第三组样例数据解释如下。

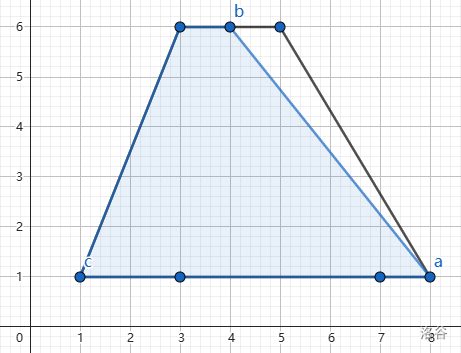
说明/提示
For the first sample test case, $Q$ is the whole triangle. Its area is $0.5$.
The second and third sample test case are shown below.

