P9593 「Daily OI Round 1」Block

给定一棵树，节点有颜色，在树上距离为 $2$ 的点连边（仍保留原来的边），求新图中颜色相同且连通的非空点集数量。由于答案可能非常大，您只需输出答案对 $10^9+7$ 取模的值。 点集连通的定义：对于图 $G(V,E)$，$V$ 的一个子集 $V'$ 是连通点集，当且仅当 $G(V',E')$ 是一个连通图，其中边集 $E'=\{(u,v)|(u,v)\in E\land u \in V'\land v\in V'\}$。

第一行一个正整数 $n$，表示节点个数。 接下来一行 $n$ 个正整数，第 $i$ 个正整数 $c_i$ 表示第 $i$ 个节点的颜色。 接下来 $n-1$ 行每行两个正整数 $u,v$ 表示原树有一条 $u$ 到 $v$ 的边。

一行一个整数，表示答案对 $10^9+7$ 取模的值。

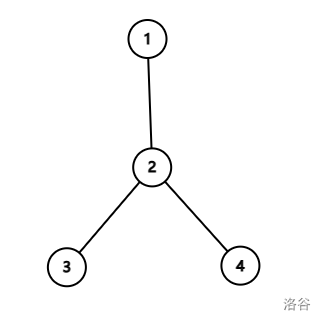
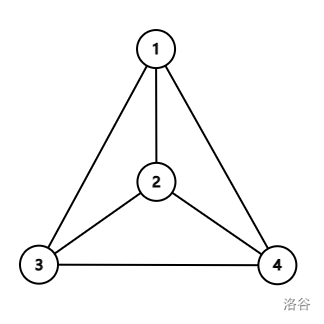
样例 1 中，原树如下图所示：  树上距离为 $2$ 的点连边后，新图如下图所示：  则 $8$ 个颜色相同且连通的非空点集分别是：$\{1\},\{2\},\{3\},\{4\},\{1,3\},\{1,4\},\{3,4\},\{1,3,4\}$。 **本题开启捆绑测试。** |$\text{Subtask}$|分值|$n \le$| 特殊性质 | 子任务依赖 | | :-----------: | :-------------:|:-----------: |:-----------: |:-----------: | |$0$|$5$|$10^5$| A | 无 | |$1$|$5$|$16$| 无 | 无 | |$2$|$5$|$10^5$| B | 无 | |$3$|$15$|$10^5$| C | 无 | |$4$|$20$|$10^5$| D | 无 | |$5$|$50$|$10^5$| 无 | $0\sim4$ | - 特殊性质 A：所有节点的颜色不相同。 - 特殊性质 B：给出的树是菊花，具体地，第 $i$ 条边连接节点 $1$ 和节点 $i+1$。 - 特殊性质 C：给出的树是链，具体地，第 $i$ 条边连接节点 $i$ 和节点 $i+1$。 - 特殊性质 D：所有节点的颜色相同。 对于全部数据，满足 $2\leq n\leq 10^5$，$1\leq c_i\leq n$。