P9616 [CERC2019] Screamers in the Storm

**题目译自 [CERC 2019](https://contest.felk.cvut.cz/19cerc/solved.html) 「[Screamers in the Storm](https://contest.felk.cvut.cz/19cerc/solved/screamers.pdf)」**

你可能不知道，每天在城市里看到的“普通”城市鸽子的正式名称其实是“岩鸽”。岩鸽 Rocky Dave 爱上了 Columba Livia——一只对岩石、鸽子及相关事物有着浓厚兴趣的年轻雌性岩鸽。一个阳光明媚的秋日下午，我们恰巧发现它们同时出现在城市郊区同一栋建筑的屋顶上。 为了炫耀自信的矫健步态，Rocky Dave 决定不直接飞向心仪对象，而是步行前往。这屋顶并非现代平顶，而是由斜坡组成的经典式样。由于建筑由多个较小结构连接而成，其平面布局略显复杂。因此，Dave 计划走向 Columba Livia 的“直线”，仅当从上方俯视时呈现笔直状态。Rocky Dave 可能需要攀爬屋脊、翻越顶峰、下到另一侧的天沟，然后再次上行，如此往复。 我们掌握了建筑精确的平面图、屋顶斜坡角度（所有角度相同），以及两位主角在屋顶的初始位置。根据这些数据，请计算 Rocky Dave 旅程的精确长度（假设 Columba Livia 在 Rocky Dave 抵达前不会离开原位）。 若路径超出建筑边界，根据 Dave 的计划，每当抵达屋顶边缘的雨水槽时，他将沿朝向 Columba Livia 的方向保持相同高度直线飞行，直至抵达建筑另一侧的雨水槽，随后继续步行旅程。 为使情境明确，现提供屋顶几何模型：设 $Z$ 为 $x$-$y$ 平面上的简单多边形（简单多边形指边界为不自交封闭曲线的多边形）。可接受金字塔指底面为 $x$-$y$ 平面上轴对齐正方形、顶点位于底面中心正上方的金字塔，其高度恰好等于底面边长的一半，且底面任意部分不得超出 $Z$ 范围。需注意，可接受金字塔的底面边长和高度可能为零，此时仅包含一个顶点（即塔尖）。 当且仅当某点 $X$（位于 $x$-$y$ 平面或上方）是可接受金字塔的顶点，且不存在 $X$ 正上方的点属于其他可接受金字塔的顶点时，该点被视为 $Z$ 的屋顶构成点。

第一行包含五个整数。第一个整数 $N\ (4\le N\le 400)$ 代表建筑平面图边缘在 $x$-$y$ 平面上构成的多边形的角点数量。随后两个整数代表 Rocky Dave 的 $x$ 和 $y$ 坐标，最后两个代表 Columba Livia 的 $x$ 和 $y$ 坐标。 接下来 $N$ 行，每行包含多边形一个角点的 $x$ 和 $y$ 坐标。所有点按逆时针方向列出。建筑的每条边均与坐标轴平行。 两只鸽子均不位于给定多边形之外。所有输入坐标均为绝对值不超过 $10^5$ 的整数。

输出 Rocky Dave 旅程的长度。答案的绝对误差或相对误差需小于 $10^{-7}$。

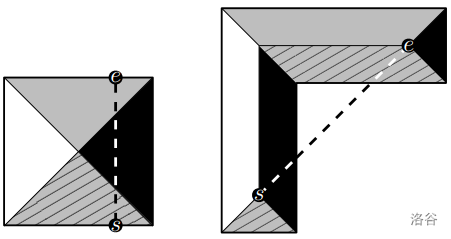
### 样例解释  翻译由 DeepSeek 生成。