P9701 [GDCPC 2023] Classic Problem

Given an undirected complete graph with $n$ vertices and $m$ triples $P_1, P_2, \cdots, P_m$ where $P_i = (u_i, v_i, w_i)$, it's guaranteed that $1 \leq u_i < v_i \leq n$, and for any two triples $P_i$ and $P_j$ with different indices we have $(u_i, v_i) \ne (u_j, v_j)$. For any two vertices $x$ and $y$ in the graph ($1 \leq x < y \leq n$), define the weight of the edge connecting them as follows: - If there exists a triple $P_i$ satisfying $u_i = x$ and $v_i = y$, the weight of edge will be $w_i$. - Otherwise, the weight of edge will be $|x - y|$. Calculate the total weight of edges in the minimum spanning tree of the graph.

There are multiple test cases. The first line of the input contains an integer $T$ ($1 \le T \le 10^5$) indicating the number of test cases. For each test case: The first line contains two integers $n$ and $m$ ($1 \leq n \leq 10^9$, $0 \leq m \leq 10^5$) indicating the number of vertices in the graph and the number of triples. For the following $m$ lines, the $i$-th line contains three integers $u_i$, $v_i$ and $w_i$ ($1 \leq u_i < v_i \leq n$, $0 \leq w_i \leq 10^9$) indicating the $i$-th triple. It's guaranteed that for all $1 \leq i < j \leq m$ we have $(u_i, v_i) \ne (u_j, v_j)$. It's guaranteed that the sum of $m$ of all test cases will not exceed $5 \times 10^5$.

For each test case output one line containing one integer indicating the total weight of edges in the minimum spanning tree of the graph.

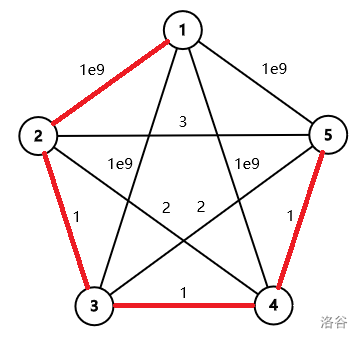
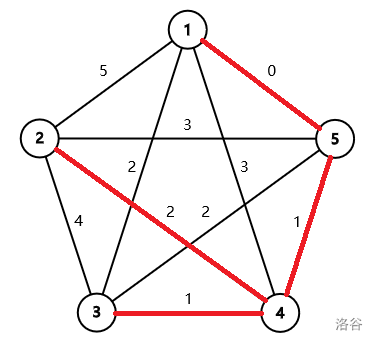
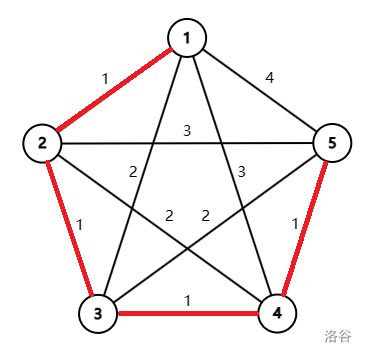
The first sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.  The second sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.  The third sample test case is illustrated as follows. The minimum spanning tree is marked by red segments.