P9702 [GDCPC 2023] Computational Geometry

给定一个有 $n$ 个顶点的凸多边形 $P$，您需要选择 $P$ 的两个顶点，并用一条同时穿过这两个顶点的直线，将 $P$ 分成两个面积均为正数的小多边形 $Q$ 和 $R$。 记 $d(Q)$ 表示多边形 $Q$ 的直径，$d(R)$ 表示多边形 $R$ 的直径，求 $(d(Q))^2 + (d(R))^2$ 的最小值。 请回忆：一个多边形的直径，指的是该多边形内部或边界上任意两点之间的距离的最大值。

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数。对于每组测试数据： 第一行输入一个整数 $n$（$4 \le n \le 5 \times 10^3$）表示凸多边形 $P$ 的顶点数量。 对于接下来 $n$ 行，第 $i$ 行输入两个整数 $x_i$ 和 $y_i$（$0 \le x_i, y_i \le 10^9$），表示凸多边形 $P$ 的第 $i$ 个顶点。顶点按逆时针顺序给出。保证该凸多边形面积为正，且没有顶点会重合。可能存在三个顶点位于同一条直线上的情况。 保证所有数据 $n$ 之和不超过 $5 \times 10^3$。

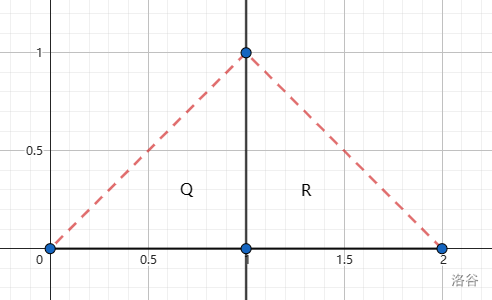
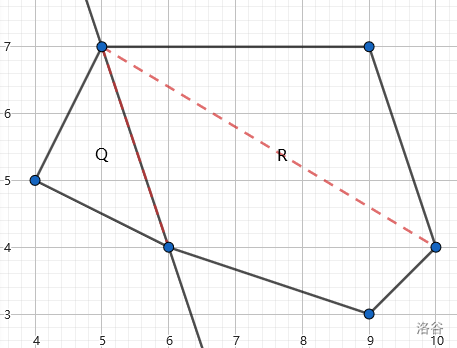
每组数据输出一行一个整数表示答案。 **【样例解释】** 第一组样例数据如下图所示。小多边形的直径用红色虚线标出。事实上，顶点 $(1, 0)$ 和 $(1, 1)$ 是这一组数据中唯一能选择的一对顶点。您不能选择顶点 $(0, 0)$ 和 $(2, 0)$，或顶点 $(0, 0)$ 和 $(1, 1)$，因为它们无法将 $P$ 分成两个面积均为正数的小多边形。  第二组样例数据如下图所示。小多边形的直径用红色虚线标出。 

The first sample test case is shown as follows. The diameter of smaller polygons are marked by red dashed segments. In fact, $(1, 0)$ and $(1, 1)$ are the only pair of vertices we can choose in this test case. You can't choose $(0, 0)$ and $(2, 0)$, or $(0, 0)$ and $(1, 1)$, because they can't split $P$ into two smaller polygons both with positive area.  The second sample test case is shown as follows. The diameter of smaller polygons are marked by red dashed segments.