P9706 「TFOI R1」Ride the Wind and Waves

Z 教授是 C 班的老师。 Z 教授最近发现一个神奇的现象，他的学生竟然都有自己暗恋的对象，但是没有一个人勇于表白。 Z 教授作为过来人，当然懂得每一个学生心里最真实纯真的想法，以及自认为的爱意情愫。Z 教授想起了初恋蕉太狼，他不想让自己的学生在青春年华失去色彩，于是 Z 教授冒着被开除的风险，主动帮助学生表达心意。 然后 Z 教授被开除了。

有一棵 $n$ 个节点的内向基环树（**保证弱连通**），树上每条边都有一个权值。现有一个特定参数 $k$。 由于基环树是内向的，所以一个点 $x$ 可能会有无法直接到达的节点。但是我们可以翻转树上的一些有向边，这样 $x$ 就可以到达树上每一个节点。如果一个节点 $x$ 需要**至少**翻转 $k$ 条边才能到达 $y$，则称 $y$ 是 $x$ 的乘风破浪点。在翻转了**最少的边**使得 $x$ 可以到达 $y$ 之后，在 $x$ 到 $y$ 的最短路径上，定义 $F(x, y)$ 为**未翻转**的边的权值之和，$R(x, y)$ 为**已翻转**的边的权值之和。 如果 $y$ 是 $x$ 的乘风破浪点，那么有一个值 $G(x, y)$ 表示 $x$ 到 $y$ 的浪涛值，定义 $G(x, y) = F(x, y) \times R(x,y)$。 请你对于每一个节点 $i$，输出 $\sum G(i, y)$ 的值，其中 $y$ 是 $i$ 的乘风破浪点。

无

无

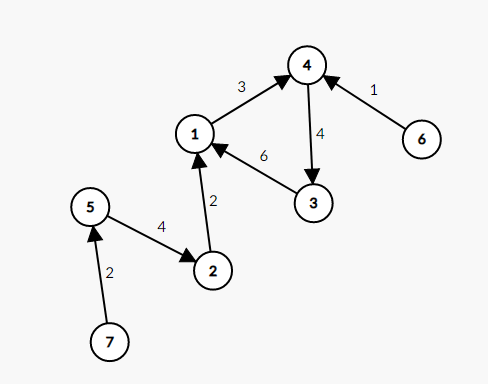
#### 样例解释 #1 拿 $3$ 节点的答案为例子，基环树的形状如图：  可知 $2,5,6,7$ 为 $3$ 的乘风破浪点，统计答案： - $G(3, 2) = 6 \times 2 = 12$。 - $G(3, 5) = 6 \times 6 = 36$。 - $G(3, 6) = 9 \times 1 = 9$。 - $G(3, 7) = 6 \times 8 = 48$。 所以 $\sum G(3, j) = 12 + 36 + 9 + 48$，答案为 $105$。 #### 数据范围 **本题采用捆绑测试**。 - Subtask 1（5 points）：$1 \leqslant n \leqslant 10$，**包含特殊性质**。 - Subtask 2（10 points）：$1 \leqslant n \leqslant 5000$，**包含特殊性质**。 - Subtask 3（25 points）：$1 \leqslant n \leqslant 10^5$，**包含特殊性质**。 - Subtask 4（60 points）：$1 \leqslant n \leqslant 10^6$，无特殊限制。 **特殊性质：保证环上节点的个数在 $10^3$ 以内。** 对于所有数据，$1 \leqslant n \leqslant 10^6$，$1 \leqslant k \leqslant 10$，保证答案不会超过 $10^{18}$。