[EC Final 2022] Map

**【题目描述】** 有一个著名的数学定理，如果你把一张公园的地图完全放在公园里，那么地图上存在一个点与它所代表的点重合。 Mio 非常喜欢这个定理，所以她把她最喜欢的公园的地图完全放在了公园里。公园 $P$ 可以用一个矩形表示。公园的地图只是一个较小（或相等）版本的公园在纸上的打印。地图与原始矩形相似。地图上的每个点都通过相似变换对应于公园中的一个点。 我们可以正式定义地图：地图是一个矩形 $M$（大小较小或相等），加上一个正实数 $r$ 和一个双射函数 $f:M \rightarrow P$，满足以下条件： - 对于 $M$ 中的每对不同的点 $a, b$，$|f(a)-f(b)|/|a-b|=r$。 这里 $|x-y|$ 表示点 $x$ 和点 $y$ 之间的欧几里德距离。 就像许多游戏一样，Mio 可以使用地图进行传送。准确地说，当 Mio 在地图上的某个点 $x$（包括边界）时，她可以传送到公园中相应的点 $f(x)$。她也可以选择不传送。反之亦然。当她在公园中的点 $y$（包括边界）时，她可以传送到代表她当前位置的地图上的点 $f^{-1}(y)$。她也可以选择不传送。 Mio 最多可以传送 $n$ 次（最少为 $0$ 次）。每次传送需要 $k$ 秒。Mio 还可以以每秒 $1$ 个单位的速度步行。 给定两个点 $s$ 和 $t$，找出 Mio 从 $s$ 到 $t$ 需要的最短时间。 每次传送可以是任意方向（从地图到公园，或从公园到地图）。地图可以倒置放置。由于地图位于公园内部，所以 Mio 可能同时在地图上和在公园中。在这种情况下，她可以选择传送的方向。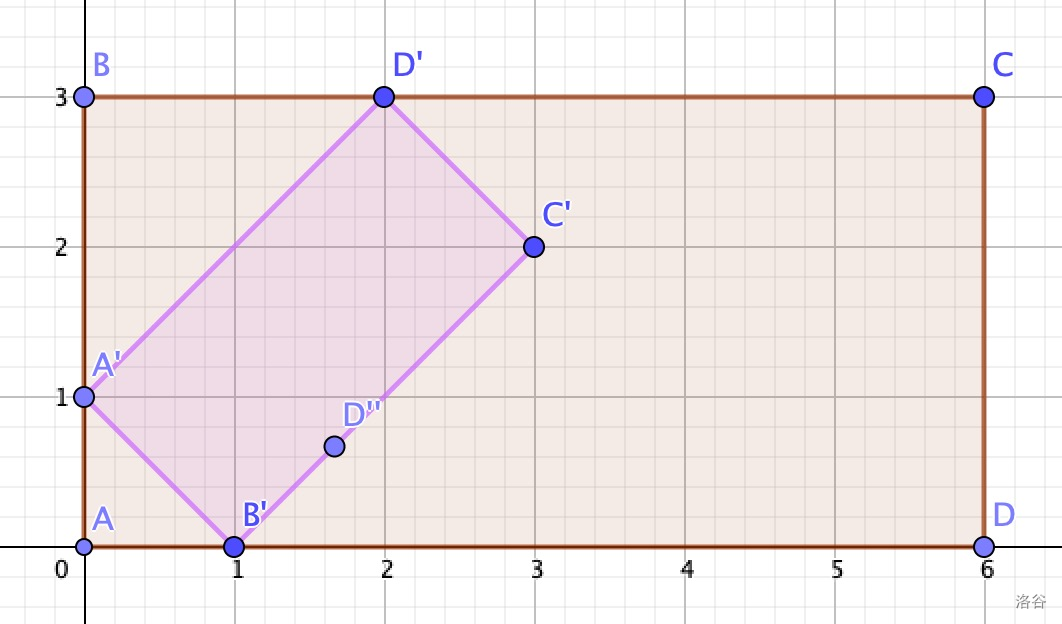 例如，在下图中，公园是 $ABCD$，地图是 $A'B'C'D'$。当 Mio 在地图上时，她同时在地图上和在公园中。当她在点 $D'$ 时，她可以从地图传送到公园（到达 $D$），并从公园传送到地图（到达 $D^{\prime\prime}$）。  **【输入格式】** 第一行包含一个整数 $T$（$1\le T\le 100$），表示测试用例的数量。 对于每个测试用例，第一行包含表示公园矩形的 $4$ 个角点。角点按顺时针或逆时针顺序给出。保证 $4$ 个角点不相同。 第二行包含表示地图矩形的 $4$ 个角点。地图的第 $i$ 个角点对应于公园的第 $i$ 个角点，对于所有 $1\le i\le 4$。请注意，您可以通过角点的顺序确定地图是否倒置放置。角点按顺时针或逆时针顺序给出。保证地图位于公园内部。（地图的边界可能与公园的边界在 $1$ 个或多个点相交。）保证地图是有效的，即存在一个正实数和一个从地图到公园的双射函数，满足上述的定义。 第三行包含两个点 $s$ 和 $t$。保证 $s$ 和 $t$ 在公园内部（或在公园的边界上）。 第四行包含两个整数 $k, n$（$0\le k\le 2\times 10^6, 0\le n\le 100$），表示每次传送所需的时间，以及最大传送次数。 输入中的每个点由一对整数表示，其绝对值不超过 $2\times 10^6$。整数之间用单个空格分隔。 **【输出格式】** 对于每个测试用例，输出一行数字表示答案。如果没有解决方案，则输出 $-1$。否则，输出最小的时间。您的答案被认为是正确的，如果其绝对或相对误差不超过 $10^{-9}$。 翻译来自于：[ChatGPT](https://chatgpt.com/)。

It is a famous math fact that if you drop a map of a park completely inside the park, then there exists a point on the map which overlays with the point it represents. Mio likes this fact a lot so she drops a map of her favorite park completely inside the park. The park $P$ can be represented by a rectangle. A map of the park is just a smaller (or equal) version of the park printed on paper. The map is similar to the original rectangle. Each point on the map corresponds to a point in the park by the similarity transformation. We can define a map formally: A map is a rectangle $M$ (of smaller or equal size) together with a positive real number $r$ and a bijective function $f:M \rightarrow P$ satisfying - For every pair of different points $a, b\in M$, $|f(a)-f(b)|/|a-b|=r$. $|x-y|$ represents the Euclidean distance between points $x$ and $y$. Like in many games, Mio can teleport using the map. Precisely, when Mio is at some point $x$ on the map (including the boundary), she may teleport to the corresponding point $f(x)$ in the park. She may also choose not to teleport. The reverse is also true. When she is at point $y$ in the park (including the boundary), she may teleport to the point $f^{-1}(y)$ on the map representing her current location. And she may also choose not to teleport. Mio can teleport at most $n$ (and at least $0$) times. Each teleport takes $k$ seconds. Mio can also walk on her foot at a speed of $1$ unit per second. Given two points $s$ and $t$, find the minimum time Mio needs to reach $t$ from $s$. Each teleport can be in any direction (from the map to the park, or from the park to the map). The map may be placed upside down. Since the map is inside the park, it is possible that Mio is on the map and in the park simultaneously. In this case, she may teleport in either direction. For example, in the following figure, the park is $ABCD$, and the map is $A'B'C'D'$. When Mio is inside the map, she is on the map and in the park simultaneously. When she is at point $D'$, she can teleport from the map to the park (reaching $D$), and from the park to the map (reaching $D^{\prime\prime}$). 

The first line contains a single integer $T$ ($1\le T\le 100$) denoting the number of test cases. For each test case, the first line contains the $4$ corners of the rectangle representing the park. The corners are given in clockwise or counterclockwise order. It is guaranteed that the $4$ corners are distinct. The second line contains the $4$ corners of the rectangle representing the map. The $i$-th corner of the map corresponds to the $i$-th corner of the park for all $1\le i\le 4$. Note that you can figure out whether the map is placed upside down or not by the order of the corners. The corners are given in clockwise or counterclockwise order. It is guaranteed that the map is inside the park. (The boundary of the map may intersect with the boundary of the park at $1$ or more points.) It is guaranteed that the map is valid, i.e., there is a positive real number and a bijective function from the map to the park satisfying the definition above. The third line contains two points $s$ and $t$. It is guaranteed that $s$ and $t$ are inside (or on the boundary of) the park. The fourth line contains two integers $k, n$ ($0\le k\le 2\times 10^6, 0\le n\le 100$), the time each teleport needs, and the maximum number of teleports. Each point in the input is represented by a pair of integers whose absolute values are no more than $2\times 10^6$. Integers are separated by single spaces.

For each test case, output one number representing the answer in one line. Your answer is considered correct if its absolute or relative error does not exceed $10^{-9}$.

2
0 0 0 2 4 2 4 0
0 0 0 1 2 1 2 0
2 1 4 2
1 1
0 0 0 3 6 3 6 0
0 1 1 0 3 2 2 3
0 0 4 2
0 3

1.0000000000
1.2272623352