P9758 [COCI 2022/2023 #3] Baltazar

Baltazar 准备去度假。他现在在 Baltazargrad，正想去 Primosten 旅游。为了抵达那里，他需要穿过许多个城市。一共有 $n$ 个城市，被 $m$ 条双向道路所联接。Baltazargrad 编号为 $1$，Primosten 编号为 $n$。 Baltazar 不确定从 Baltazargrad 去 Primosten 的路线，所以他将会使用 GPS，这会指引他以最短路线抵达。 但 Blatazar 真的很爱旅游，而且他可以将魔法药水使用在任何一条路上（即使他没有经过），从而将路的长度增长 $2$ 千米。但他仅能使用一次药水。 不久他意识到，他必须在中午之前在 Primosten 的 Zora 旅馆入住。所以他不能过分增加最短路的总长度。他现在想知道，一共有多少条路可以让他使用药水，使得最短路的长度恰好增加 $1$ 千米。

多组数据。 第一行一个整数 $t$，表示数据组数。 接下来对于每组数据，第一行两个整数 $n,m$，分别表示城市的数量和城市之间道路的数量。 接下来的 $m$ 行，每行三个整数 $a_i,b_i,w_i$，表示一条连接城市 $a_i,b_i$ 且长度为 $w_i$ 的道路。两个城市间最多只有一条道路。 保证所有城市是相互联通的。也就是说，任何一对城市，都有一条相互可达的路径，但不一定是直接相连。 保证所有数据的 $n, m$ 各自之和均不超过 $300000$。

第一行输出一个整数 $c$，表示 Baltazar 可以使用魔法药水的道路数量。 接下来一行 $c$ 个整数，以编号升序输出所有满足条件的道路。

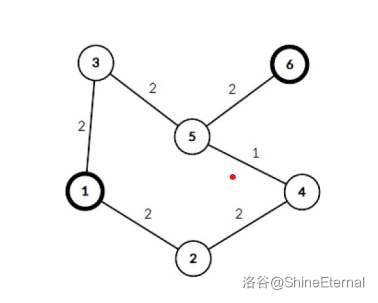
**【样例解释】** 城市和道路如图所示。如果 Baltazar 把他的魔法药水使用在第二条道路上（连接城市 $3$ 和 $5$ 的），那么城市 $1$ 和 $n$ 之间最短的距离将会增加 $1$。  **【数据范围】** | 子任务 | 分值 | 特殊性质 | | :----------: | :----------: | :----------: | | $1$ | $15$ | $n,m \leq 1000$ | | $2$ | $30$ | 有一条在起点终点之间的道路，这条道路的长度满足恰好比两个城市之间的最短路线长 $1$ 千米。 | | $3$ | $65$ | 无特殊性质 | 对于 $100\%$ 的数据，满足 $1\le t \le 10000,2\leq n \leq 3\times10^5,1\le m\le \min(3\times 10^5,\dfrac{n\times (n-1)}{2}), 1\le a_i,b_i\le n,a_i\neq b_i,1\le w_i\le 10^9$。 本题满分 $110$ 分。