P9794 [NERC 2018] Distance Sum

翻译自 [NERC 2018](https://neerc.ifmo.ru/archive/2018/neerc-2018-statement.pdf) D 题。

给你一个 $n$ 个顶点 $m$ 条边的连通无向图，定义 $u$ 与 $v$ 的距离 $d(u, v)$ 为从 $u$ 到 $v$ 最短路径上经过的边数。 现在请你求出 $\sum_{u=1}^n \sum_{v=u+1}^n d(u,v)$。

第一行给定两个整数 $n(1 \leq n \leq 10^5)$，$m(n - 1 \leq m \leq n + 42)$，分别表示点数和边数。 接下来 $m$ 行，每行 $2$ 个整数 $x_i$ 和 $y_i(1 \leq x_i,y_i \leq n, x_i \neq y_i)$，表示 $x_i$ 和 $y_i$ 之间有一条边。 保证没有重边和自环。

输出 $\sum_{u=1}^n \sum_{v=u+1}^n d(u,v)$。

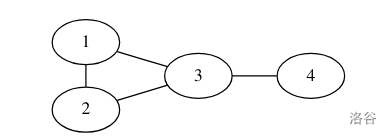
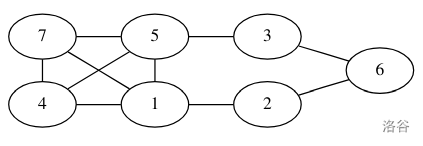
对于所有数据保证 $1 \leq n \leq 10^5$，$n-1 \leq m \leq n + 42$，$1 \leq x_i, y_i \leq n$ 且 $x_i \neq y_i$。 样例一的图是：  其中 $d(1,2) = 1$，$d(1,3) = 1$，$d(1,4) = 2$，$d(2,3) = 1$，$d(2,3) = 2$，$d(3,4) = 1$，总和为 $1 + 1 + 2 + 1 + 2 + 1 = 8$。 样例二为：