P9803 [NERC 2018] Minegraphed

翻译自 [NERC 2018](https://neerc.ifmo.ru/archive/2018/neerc-2018-statement.pdf) M 题。

Marika 正在制作一款名为 Minegraphed 的游戏，游戏内容是你在一个三维的长方体上移动。长方体游戏场地的每个单元格都是空单元格或障碍单元格。你总是在一个空单元格里面，要么在最底层，要么在一个障碍的顶部。对于每次移动，你可以选择东南西北中的一项进行移动，移动的规则如下： - 你不能移动至矩形立方体外面。 - 如果你面前的单元格是空的，那么你可以向前移动一格，然后向底部落下，直到你到达最底层或者一个障碍。 - 如果你在非最顶层，你前面的单元格是一个障碍物，你上面的单元格和这个障碍物上面的单元格都是空的，然后你可以爬到该障碍物的顶部。 - 其余情况，你不能进行移动。 长方体中有 $n$ 个可以站立的特殊空单元格，分别编号为 $1\sim n$。 Marika 还有一个 $n \times n$ 的二维数组 $a$，表示一个包含 $n$ 个结点的有向图的邻接矩阵（$a_{i,j}=1$ 表示有一条边 $i\to j$，反之亦然）。你需要满足 $i$ 在有向图上能通过若干条边到达 $j$，当且仅当在长方体的游戏场地中可以通过移动从编号为 $i$ 的单元格到达编号为 $j$ 的单元格。 请构造一种合法方案。

第一行一个整数 $n \ (1 \leq n \leq 9)$。 然后 $n$ 行，每行 $n$ 个数分别为 $a_{i,1},a_{i,2},\ldots,a_{i,n}$，表示有向图的邻接矩阵。

输出第一行 $x,y,z$ 表示你的矩形立方体的长宽高，你需要保证 $x \times y \times z \leq 10^6$。 然后 $z$ 层（自上向下），每层一个 $x \times y$ 的矩形：$map_{i,j}$ 若为 `#` 表示障碍，若为 `.` 表示普通的空单元格，若为数字则表示一个特殊空单元格，数字表示其对应的编号。 保证存在解法。

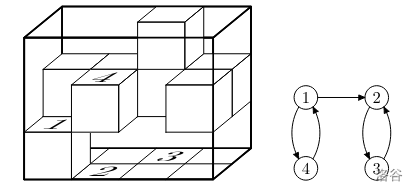
样例解释：  对于所有数据保证 $1 \leq n \leq 9$，$a_{i,j} \in \{0, 1\}$。