P9827 [ICPC 2020 Shanghai R] Sky Garden

杜教授和庞教授计划在 Allin 市附近建造一个空中花园。在花园中，将有一个由直路和环形路组成的植物迷宫。 在植物迷宫的蓝图上，杜教授画了 $n$ 个圆，表示环形路。所有圆的圆心都是 $(0, 0)$。第 $i$ 个圆的半径是 $i$。 同时，庞教授在蓝图上画了 $m$ 条直线，表示直路。所有的直线都经过 $(0, 0)$。每个圆被这些直线等分成 $2m$ 个部分。 设 $Q$ 为 $n+m$ 条道路的集合。设 $P$ 为 $Q$ 中两条不同道路的所有交点的集合。注意，每条环形路和每条直路都有两个交点。 对于两个不同的点 $a \in P$ 和 $b \in P$，我们定义 $dis(\{a, b\})$ 为沿着道路从 $a$ 到 $b$ 需要走的最短距离。请计算对于所有 $\{a, b\} \subseteq P$ 的 $dis(\{a, b\})$ 的和。

唯一一行包含两个整数 $n,m~(1\le n,m\le 500)$。

输出一个数字——$P$ 中每对点之间距离的总和。 你的答案被认为是正确的，如果其绝对误差或相对误差不超过 $10^{-6}$。

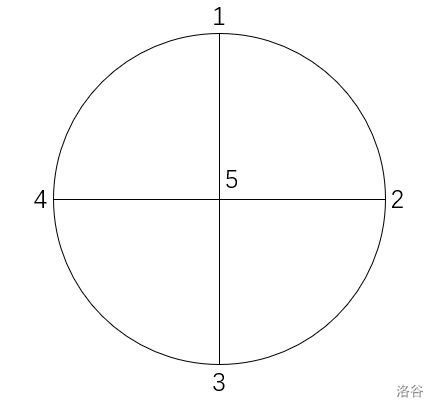
 $dis(p_1, p_2)=dis(p_2, p_3)=dis(p_3, p_4)=dis(p_1, p_4)=\frac{\pi}{2}$ $dis(p_1, p_5)=dis(p_2, p_5)=dis(p_3, p_5)=dis(p_4, p_5)=1$ $dis(p_1, p_3)=dis(p_2, p_4)=2$。 题面翻译由 ChatGPT-4o 提供。