P9846 [ICPC 2021 Nanjing R] Paimon's Tree

Paimon has found a tree with $(n + 1)$ initially white vertices in her left pocket and decides to play with it. A tree with $(n + 1)$ nodes is an undirected connected graph with $n$ edges. Paimon will give you an integer sequence $a_1, a_2, \cdots, a_n$ of length $n$. We first need to select a vertex in the tree and paint it black. Then we perform the following operation $n$ times. During the $i$-th operation, we select a white vertex $x_i$ which is directly connected with a black vertex $y_i$ by an edge, set the weight of that edge to $a_i$ and also paint $x_i$ in black. After these $n$ operations we get a tree whose edges are all weighted. What's the maximum length of the diameter of the weighted tree if we select the vertices optimally? The diameter of a weighted tree is the longest simple path in that tree. The length of a simple path is the sum of the weights of all edges in that path.

There are multiple test cases. The first line of the input contains an integer $T$ ($1 \le T \le 5 \times 10^3$) indicating the number of test cases. For each test case: The first line contains an integer $n$ ($1 \le n \le 150$) indicating the length of the sequence. The second line contains $n$ integers $a_1, a_2, \cdots, a_n$ ($1 \le a_i \le 10^9$) indicating the sequence. For the following $n$ lines, the $i$-th line contains two integers $u_i$ and $v_i$ ($1 \le u_i, v_i \le n + 1$) indicating that there is an edge connecting vertex $u_i$ and $v_i$ in the tree. It's guaranteed that there is at most $10$ test cases satisfying $n > 20$.

For each test case output one line containing one integer indicating the maximum length of the diameter of the tree.

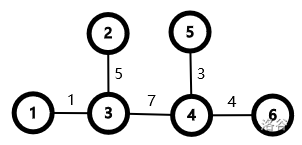
For the first sample test case, we select the vertices in the order of $1, 3, 4, 5, 2, 6$, resulting in the weighted tree of the following image. It's obvious that the longest simple path is of length $16$.