P9864 [POI 2021/2022 R2] age
题目背景
翻译自 [POI2021~2022R2 Day1T1](https://szkopul.edu.pl/problemset/problem/weKRWGa1NgLNHT1WLDo5ohuH/statement/)。
题目描述
有一个 $n$ 个城市的国家,我们可以将其看为一棵 $n-1$ 条道路连接的树,有一天,你突发奇想,想要派出 $k$ 个人在不同城市上。人及其移动需要满足如下条件:
- 每天只能是一个人移动,移动到其相邻存在道路连接一个城市。
- 假如有两个人 $a,b$,城市 $i$ 被 $a$ 到达过了,则 $b$ 不能到达 $i$ 城市。
初始时你知道了人的位置,每个人初始所在地不相同,且该城市视为“已到达过”的城市,你需要安排一个合法的经过城市的方案。
请你求出最少要几天才能使所有的城市都被人到达过。
输入格式
第一行两个整数 $n,k\ (1 \leq n \leq 5 \times 10^5, 1 \leq k \leq n)$。
第二行 $k$ 个数,表示那些人的初始位置。
然后 $n-1$ 行,描述了每条道路 $(a_i,b_i)\ (1 \leq a_i,b_i \leq n)$。
输出格式
输出最少天数。
说明/提示
样例解释:
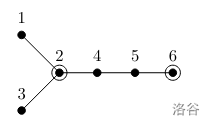
子任务分配如下:
| 子任务编号 | 特殊性质 | 分值 |
| :----------: | :----------: | :----------: |
| $1$ | $n \leq 10$ | $6$ |
| $2$ | $n \leq 20$ | $13$ |
| $3$ | $n \leq 2000$ | $27$ |
| $4$ | $k=1$ | $10$ |
| $5$ | $k=2$ | $7$ |
| $6$ | 输入为一条链 | $7$ |
| $7$ | 无特殊性质 | $30$ |
子任务 $0$ 为样例。