P9885 [ICPC 2018 Qingdao R] Sequence and Sequence

Consider the following two sequences $P$ and $Q$. We denote $P(i)$ as the $i$-th element in sequence $P$, and $Q(i)$ as the $i$-th element in sequence $Q$: - Sequence $P$ is a $\textbf{sorted}$ sequence where for all $k \in \mathbb{Z^+}$, $k$ appears in sequence $P$ for $(k+1)$ times ($\mathbb{Z^+}$ is the set of all positive integers). 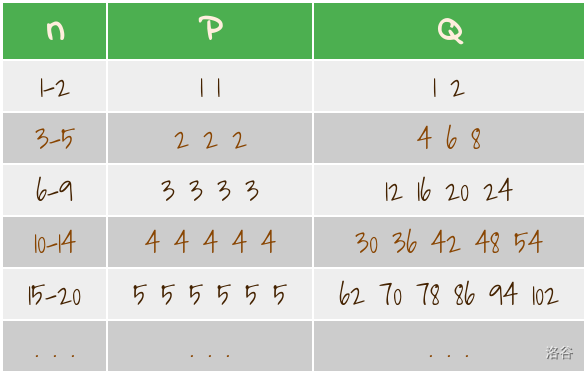That is to say, $P = \{1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, \dots \}$ - Sequence $Q$ can be derived from the following equations: $$\begin{cases} Q(1) = 1 & \\ Q(i) = Q(i-1) + Q(P(i)) & \text{if } i > 1 \end{cases}$$ That is to say, $Q = \{1, 2, 4, 6, 8, 12, 16, 20, 24, 30, 36, 42, 48, 54, 62, \dots \}$  Given a positive integer $n$, please calculate the value of $Q(n)$.

There are multiple test cases. The first line of the input contains an integer $T$ (about $10^4$), indicating the number of test cases. For each test case: The first and only line contains an integer $n$ ($1 \le n \le 10^{40}$).

For each test case output one line containing one integer, indicating the value of $Q(n)$.