P9892 [ICPC 2018 Qingdao R] Mirror

在一个无限二维平面上包含一个不透明障碍物和一个单面镜子。障碍物被表示为一个三角形，而镜子被表示为一个从点 $(x_{m,1}, y_{m,1})$ 指向 $(x_{m,2}, y_{m,2})$ 的有方向的线段，线段的右侧是反射面。 有 $m$ 个石头位于点 $(x_1,y_1)$，DreamGrid 希望将所有石头移动到点 $(x_2,y_2)$。需要满足以下条件： DreamGrid 每次只能携带一个石头。 一旦 DreamGrid 拿起一个石头，他只能将其放置在点 $(x_2,y_2)$。 设 $L$ 为 DreamGrid 走过的路径，对于路径上的每一个点 $p$，DreamGrid 必须能直接或通过镜子看到所有的石头。 **注意：** 如果视线的某部分在障碍物内（视线穿过障碍物的点或边界是允许的），则认为 DreamGrid 无法通过这条视线看到石头。 如果镜子的一个端点在视线上，认为 DreamGrid 既可以在镜子中看到石头，也可以透过镜子看到石头。 反射过程遵循物理规律：入射角等于反射角。入射光线和反射光线在镜子的同一侧。 如果视线与镜子平行，则不发生反射，镜子不被视为障碍物。 DreamGrid 不能移动进入障碍物，但可以在障碍物的边缘或顶点上移动。 DreamGrid 不能穿过镜子移动，但可以在镜子上移动。注意，如果 DreamGrid 在镜子的线段上（不包括两个端点），他只能看到他来的那一侧，并且不能透过镜子看到。 DreamGrid 想要知道移动所有石头从 $(x_1,y_1)$ 到 $(x_2, y_2)$ 的最短距离。

输入包括多个测试用例。第一行是一个整数 $T$（大约 100），表示测试用例的数量。对于每个测试用例： 第一行包含一个整数 $m$（$1 \le m \le 10^6$），表示石头的数量。 第二行包含四个整数 $x_1$, $y_1$, $x_2$ 和 $y_2$，表示起始点和目标点。 第三行包含四个整数 $x_{m,1}$, $y_{m,1}$, $x_{m,2}$ 和 $y_{m,2}$，表示镜子的坐标。 接下来的 $3$ 行，每行包含两个整数 $x_i$ 和 $y_i$，表示障碍物顶点的坐标。 所有坐标的绝对值不超过 $100$。起始点和目标点都在障碍物和镜子之外。镜子和障碍物没有公共点。 保证没有三个点是共线的。

输出对于每个测试用例，输出一个实数表示最短距离，如果 DreamGrid 无法在约束条件下移动所有石头，则输出 $-1$。 如果你的答案的绝对误差或相对误差小于 $10^{-6}$，则认为你的答案是正确的。

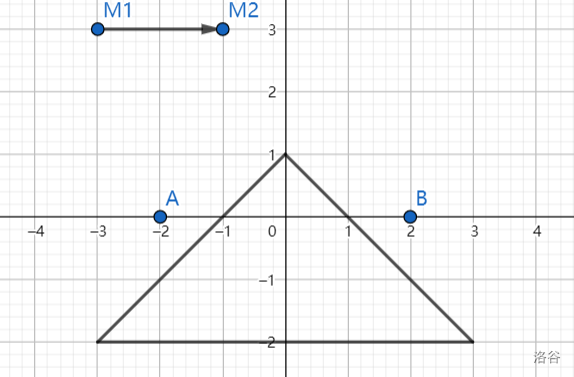
We now welcome our special guest Mashiro, who heartily donates this problem to our problemset, to explain the sample test cases for us using her sketch book.    $\textit{(Image from pixiv. ID: 32084305)}$ In the figures above, we indicate the start point as point $A$ and the target point as point $B$. The mirror is indicated by the line segment pointing from $M1$ to $M2$, with the right side being reflective. For the first sample test case, the optimal path is $A \to C \to B \to C \to A \to C \to B$. For the second sample test case, as DreamGrid cannot see $A$ from $B$, it's impossible to move all the two stones from $A$ to $B$ while following the constraints in the problem description.