[ICPC2018 Qingdao R] Sub-cycle Graph

### 题目描述 对于一个有 $n(n\ge3)$ 个点和 $m$ 条边的无向简单图，其中点的编号为 $1$ 到 $n$。如果加非负整数条边能使这个图是变为 $n$ 个点的简单环，我们称这个是一个 “半环” 图。 给定两个整数 $n$ 和 $m$，你的任务是计算有多少个**不同的** $n$ 个点，$m$ 条边的 “半环” 图。考虑到答案会很大，请将答案模 $10^{9} + 7$ 的结果输出。 定义 - 一个简单图是指一个没有自环和重边的图； - $n$ 个点的 “简单环” 是指任意一个有 $n$ 个点和 $n$ 条边的无向简单连通图，其中所有点的度均为 $2$； - 如果两个有着 $n$ 个点和 $m$ 条边的无向简单图是不同的，那么它们具有着不同的边集； - 现在有两个点 $u$ 和 $v(u < v)$，记 $(u,v)$ 表示连接 $u,v$ 两点的无向边。两条无向边 $(u_1,v_1)$ 和 $(u_2,v_2)$ 如果是不同的，那么 $u_1\ne u_2$ 或 $v_1\ne v_2$。 ### 输入格式 此题有多组数据。 第一行有一个整数 $T$（约为 $2\times 10^{4}$），指测试用例的数量。对于每组数据： 一组数据只有一行，两个整数 $n$ 和 $m$（$3 \le n \le 10^{5}$，$0\le m \le \frac{n(n-1)}{2}$），表示图的点数和边数。 $n$ 的总和不超过 $3\times 10^{7}$。 ### 输出格式 对于每组数据，你只需要输出一行表示答案。

Given an undirected simple graph with $n$ ($n \ge 3$) vertices and $m$ edges where the vertices are numbered from 1 to $n$, we call it a ``sub-cycle`` graph if it's possible to add a non-negative number of edges to it and turn the graph into exactly one simple cycle of $n$ vertices. Given two integers $n$ and $m$, your task is to calculate the number of different sub-cycle graphs with $n$ vertices and $m$ edges. As the answer may be quite large, please output the answer modulo $10^9+7$. Recall that - A simple graph is a graph with no self loops or multiple edges; - A simple cycle of $n$ ($n \ge 3$) vertices is a connected undirected simple graph with $n$ vertices and $n$ edges, where the degree of each vertex equals to 2; - Two undirected simple graphs with $n$ vertices and $m$ edges are different, if they have different sets of edges; - Let $u < v$, we denote $(u, v)$ as an undirected edge connecting vertices $u$ and $v$. Two undirected edges $(u_1, v_1)$ and $(u_2, v_2)$ are different, if $u_1 \ne u_2$ or $v_1 \ne v_2$.

There are multiple test cases. The first line of the input contains an integer $T$ (about $2 \times 10^4$), indicating the number of test cases. For each test case: The first and only line contains two integers $n$ and $m$ ($3 \le n \le 10^5$, $0 \le m \le \frac{n(n-1)}{2}$), indicating the number of vertices and the number of edges in the graph. It's guaranteed that the sum of $n$ in all test cases will not exceed $3 \times 10^7$.

For each test case output one line containing one integer, indicating the number of different sub-cycle graphs with $n$ vertices and $m$ edges modulo $10^9+7$.

3
4 2
4 3
5 3

15
12
90

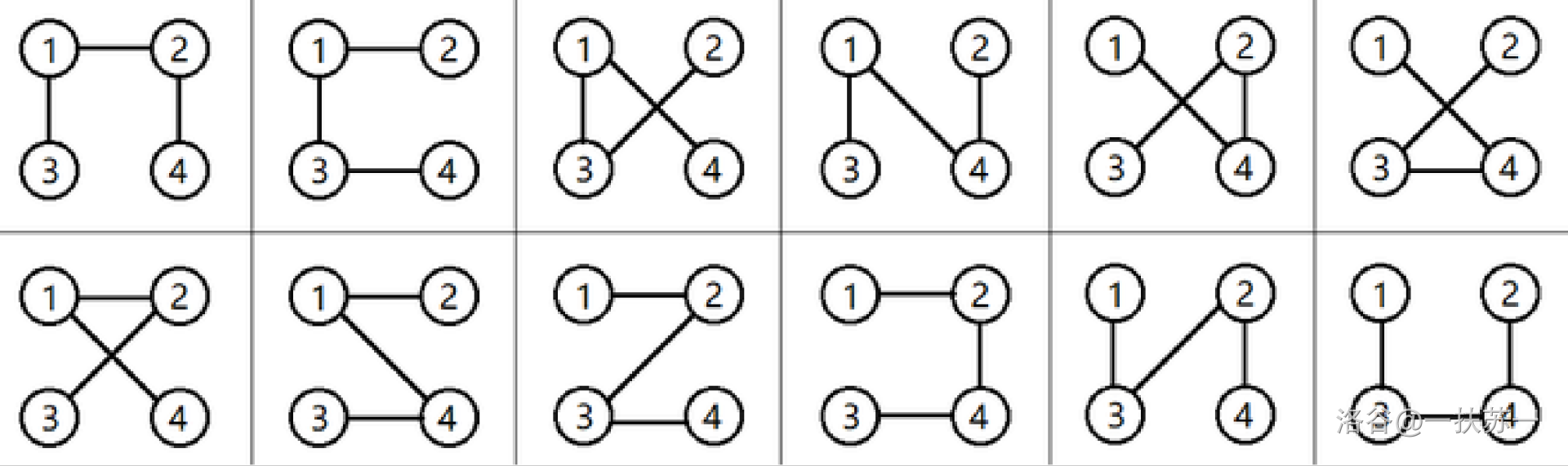
The 12 sub-cycle graphs of the second sample test case are illustrated below.