P9897 [ICPC 2018 Qingdao R] Function and Function

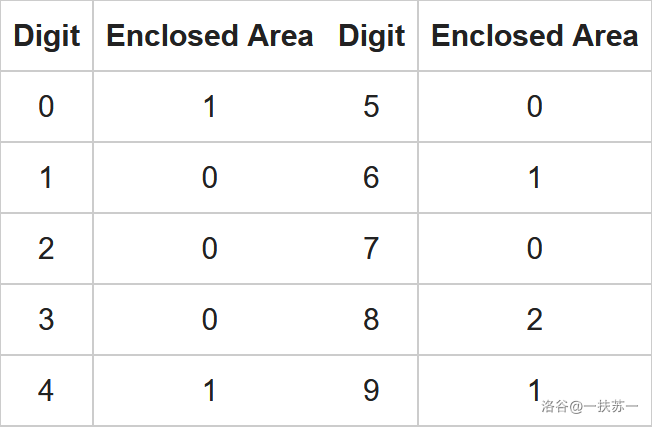
If we define $f(0) = 1, f(1) = 0, f(4) = 1, f(8) = 2, f(16) = 1, \dots$, do you know what function $f$ means? Actually, $f(x)$ calculates the total number of enclosed areas produced by each digit in $x$. The following table shows the number of enclosed areas produced by each digit:  For example, $f(1234) = 0 + 0 + 0 + 1 = 1$, and $f(5678) = 0 + 1 + 0 + 2 = 3$. We now define a recursive function $g$ by the following equations: $$\begin{cases} g^0(x) = x \\ g^k(x) = f(g^{k-1}(x)) & \text{if } k \ge 1 \end{cases}$$ For example, $g^2(1234) = f(f(1234)) = f(1) = 0$, and $g^2(5678) = f(f(5678)) = f(3) = 0$. Given two integers $x$ and $k$, please calculate the value of $g^k(x)$.

There are multiple test cases. The first line of the input contains an integer $T$ (about $10^5$), indicating the number of test cases. For each test case: The first and only line contains two integers $x$ and $k$ ($0 \le x, k \le 10^9$). Positive integers are given without leading zeros, and zero is given with exactly one `0'.

For each test case output one line containing one integer, indicating the value of $g^k(x)$.