SP1004 POLYCODE - Polygon Encoder
题目描述
想象一张无限大的表格,行和列都用自然数编号。下图展示了一种方法,按顺序为每个表格单元格分配一个自然数:
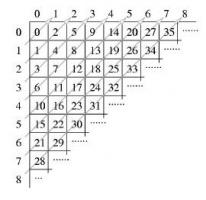
这种单元格的枚举方法能够用自然数来表示复杂的数据类型:
- 一个自然数对 (i, j) 可以通过表中第 i 行第 j 列的编号来表示。例如,数对 (3, 2) 对应的自然数是 17,记作 P2(3, 2) = 17。
- 这种表示方法也可以用于更高维度的 n 元组。比如,三元组 (a, b, c) 可以表示为 P2(a, P2(b, c))。四元组 (a, b, c, d) 可以表示为 P2(a, P2(b, P2(c, d)))。这个过程可以推广到任意 n:Pn(a1, ..., an) = P2(a1, Pn−1(a2, .., an)),其中 Pn 是n元组表示函数,n ≥ 2。举个例子,P3(2, 0, 1) = 12。
- 任意长度的列表 ha1, ..., ani 则可以表示为
L(ha1, ..., ani) = P2(n, Pn(a1, ..., an))。
例如,L(h0, 1i) = 12。
凸形制造者协会(ACM)在多边形表示系统中使用了这种巧妙的自然数编码方式。这个系统可以通过一个自然数来表示由整数坐标定义的多边形。具体来说,给定一个由顶点序列 h(x1, y1), ..., (xn, yn)i 构成的多边形,可以表示为:
L((hP2(x1, y1), ..., P2(xn, yn)))。
ACM 需要一个程序,可以通过给定的自然数表示的多边形来计算其面积。保证给定的多边形是简单多边形,也就是说,它的边不会相交。
例如,拥有顶点 (1,1), (2,0) 和 (0,0) 的三角形其编码为 2141。这个三角形的面积是 1。
输入格式
每个输入由多个测试用例组成。每个测试用例在独立的一行中给出,表示一个多边形的自然数。输入以 * 符号结束。
输出格式
每个测试用例输出一行,依照输入顺序。每行包含一个十进制数,表示对应编码的多边形的面积。输出结果保留1位小数,舍去不重要的尾数。
**本翻译由 AI 自动生成**