SP10732 TRAPEZBO - Trapezoid
题目描述
平面直角坐标系内,有两条平行于X轴的直线。在两条直线内有一些梯形,每个梯形上底的两个顶点都落在上面的直线,下底的两个顶点都落在下面的直线(见下图)。
我们用 $ A_i,B_i,C_i,D_i $ 分别表示第i个梯形的左上角,右上角,左下角,右下角。如果一个梯形集合内,任意两个梯形不相交,则被称为独立梯形子集S。
# 任务
找到最大的独立梯形子集(子集中梯形个数最多),还要找到具有不同的最大独立梯形子集的个数。个数模 30013。
输入格式
第一行包含一个整数 $ n (1 \leq n \leq 100,000) $ 表示梯形的个数
接下来的n行,每行4个整数$ A_i,B_i,C_i,D_i (1 \leq A_i,B_i,C_i,D_i \leq 1,000,000,000) $ 。任意两个梯形都没有共同的顶点(角)。
输出格式
输出两个整数,第一个是最大的独立梯形子集,第二个是不同的最大独立梯形子集的个数模30013。
# 样例解释
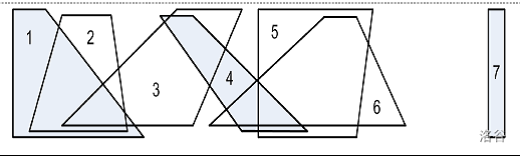
上图并不是样例的精确表示,梯形的上边和下边分别被下移和上移以便于观察。
最大独立子集梯形个数是3,不同的最大独立梯形子集的个数是8。
编号 1,4,7; 1,5,7; 1,6,7;
编号 2,4,7; 2,5,7; 2,6,7;
编号 3,5,7; 3,6,7;