SP12364 TAP2012A - Awari 2

Awari 是一种来自安的列斯群岛的一人棋类游戏，使用盒子和石子进行。这种游戏的一个变种使用 **N** 个编号为 **1** 到 **N** 的盒子。游戏开始时，每个盒子里有若干石子。规则非常简单，玩家只需要进行以下一种有效操作：从编号为 **i** 且石子数恰好为 **i** 的盒子中取出所有石子，然后将这些石子中的每一颗放入编号 **1** 到 **i-1** 的盒子中，每个盒子放置一颗；最后一颗石子由玩家保留。只要存在编号为 **i** 且石子数恰好为 **i** 的盒子，玩家就可以继续进行操作。当不再符合条件的盒子存在时，游戏结束。如果在这时所有盒子都是空的，玩家获胜；否则，玩家失败。 下图展示了一个可能的游戏初始状态，其中有 **N = 5** 个盒子（用圆形表示），分别包含 **P$_{1}$ = 0**, **P$_{2}$ = 1**, **P$_{3}$ = 3**, **P$_{4}$ = 0** 和 **P$_{5}$ = 2** 颗石子（用黑点表示）。如果选择编号为 **3** 且含有 **3** 颗石子的盒子进行移动，结果就会变成右侧所示的状态，且玩家手中会多一颗石子。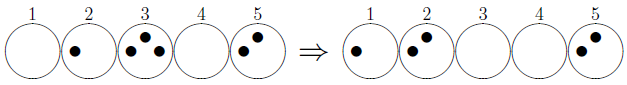  现在，给定盒子的初始状态，你需要判断是否可以通过一系列有效操作令所有盒子清空，从而赢得游戏。

每个测试用例有两行描述。第一行包含一个整数 **N**，表示盒子的数量（$1 \le N \le 500$）。第二行包含 **N** 个整数 **P$_{i}$**，表示从盒子 **1** 到盒子 **N** 的初始石子数量（$0 \le P_i \le 500$ 对于 $i = 1, \ldots, N$）。每个测试用例中至少有一个盒子非空，即存在某个 **i** 满足 **P$_{i}$ \ ≠ 0**。输入以一行 **-1** 结束。

对于每个测试用例，输出一行，包含一个字符。如果可以赢得游戏，输出大写字母 `S`；否则，输出大写字母 `N`。 **本翻译由 AI 自动生成**