SP131 SQDANCE - Square dance

You are hired by french NSA to break the RSA code used on the Pink Card. The easiest way to do that is to factor the public modulus and you have found the fastest algorithm to do that, except that you have to solve a subproblem that can be modeled in the following way. Let 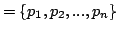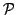be a set of prime numbers. If 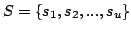 and 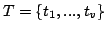 are formed with elements of 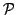, then S\*T will denote the quantity 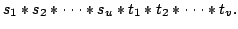 We call relation a set of two primes p,q, where p and q are distinct elements of 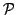. You dispose of a collection of R relations 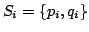 and you are interested in finding sequences of these, 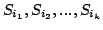 such that 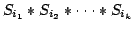 is a perfect square. The way you look for these squares is the following. The ultimate goal is to count squares that appear in the process. Relations arrive one at a time. You maintain a collection 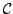 of relations that do not contain any square subproduct. This is easy: at first, 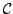 is empty. Then a relation arrives and 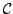 begins to grow. Suppose a new relation 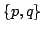 arrives. If no square appears when adding 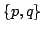 to , then 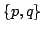 is added to the collection. Otherwise, a square is about to appear, we increase the number of squares, but we do not store this relation, hence 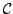 keeps the desired property. Let us consider an example. First arrives 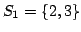 and we put it in 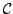; then arrives 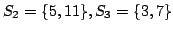 and they are stored in 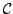. Now enters the relation 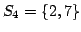. This relation could be used to form the square: 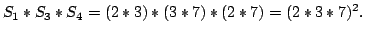 So we count 1 and do not store 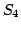 in 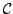. Now we consider 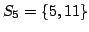 that could make a square with 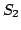, so we count 1 square more. Then 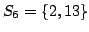 is put into 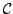. Now 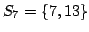 could make the square 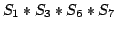. Eventually, we get 3 squares.

The first line of the input contains a number T

For each test case, output the number of squares that can be formed using the preceding rules.