SP14055 WWAKER - The Wind Waker

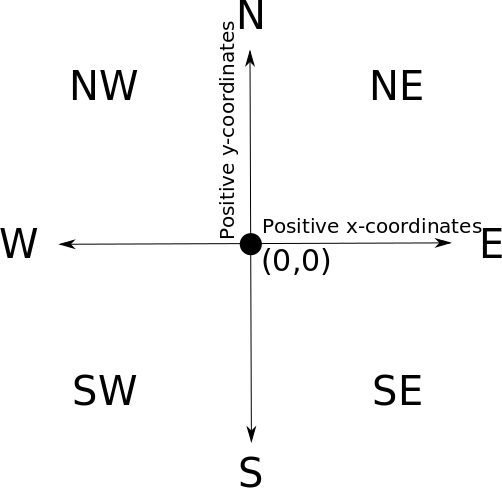
世界再次面临危机，而林克就是那个拯救世界的英雄！为了成功，他需要跨越大海，收集一些传说中的神器。 大海被看作是一个无限的二维平面，采用笛卡尔坐标系，(0, 0) 是海洋的中心。基本方位如图所示：  林克得依靠他的船来旅行，但船只能跟随风的方向前进。例如，风往北吹时，他只能向北航行；倘若没有风，他就无法移动。 然而，林克有「风之杖」这件魔法道具。通过这支魔法棒，林克能弹奏「风之歌」，这首神秘的旋律可以让他操控风向。每次使用风之杖，林克可以选择让风停下来（用字母 X 表示），或者让风吹向八个基本方位之一（北 N，南 S，东 E，西 W，东北 NE，东南 SE，西南 SW，西北 NW）。  林克利用风之杖 林克的任务是到达坐标 (x $_{2}$, y $_{2}$) 并在那里停下来，来收集传说中的物品。他现在位于坐标 (x $_{1}$, y $_{1}$)，起始时无风。需要为他规划一条从 (x $_{1}$, y $_{1}$) 到 (x $_{2}$, y $_{2}$) 的路径。路径由数次在特定位置使用风之杖的动作组成。比如，从 (0, 0) 到 (1, 1) 的一种路径如下： 1. 在 (0, 0) 点，令风向北吹； 2. 在 (0, 1) 点，令风向东吹； 3. 在 (1, 1) 点，令风停止。 规划的路径需满足以下条件： - 尽量减少林克使用风之杖的次数； - 如果使用次数相同，则应尽量缩短总航行距离； - 如果总距离也相同，应选择字典序较小的风向变化序列。字典序规则为：_E < N < NE < NW < S < SE < SW < W < X_。例如，风向先变为 N，然后变为 SW，再变为 W 的路径优于风向先变为 N，然后变为 W，再变为 E，因为 _(N, NW, W)_ 在字典序上小于 _(N, W, E)_（因为 _N=N, NW < W_）。 请参照样例输入和输出。 **注意**：「林克」、「风之杖」和上述部分图片的版权属于 **Nintendo (r)**。作者仅仅想通过这些元素让问题更有趣，作者支持 **Nintendo**！

输入由一个或多个测试用例组成。每个测试用例在一行内给出四个整数 x $_{1}$, y $_{1}$, x $_{2}$, y $_{2}$ ，它们的值范围为 -10万到10万。文件以 EOF 结束。

对每个测试用例，先输出一行整数 K，表示使用风之杖的次数。接下来，输出 K 行，格式为 _x $_{i}$ y $_{i}$ D_，表示在坐标 (x $_{i}$, y $_{i}$) 处调整风向为 D。坐标需精确到小数点后两位，D 可以是 'S', 'N', 'W', 'E', 'SE', 'SW', 'NE', 'NW' 或 'X'。请按路径中事件发生的顺序输出。 接着输出总航行距离，保留三位小数。每个测试用例输出完成后加一空行。请参阅样例输出。 **本翻译由 AI 自动生成**