SP14055 WWAKER - The Wind Waker

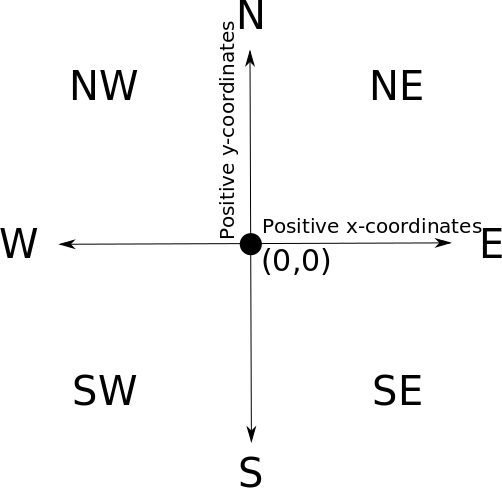
The world is in danger once again, and Link is the hero who will save us! In order to save the world, Link must travel overseas and collect some legendary items. The sea can be described as an infinite 2D plane with a Cartesian coordinate system, in which the point (0,0) denotes the center of the sea. Also, the cardinal directions are defined as usual:  Link must use his boat to travel. Unfortunately, Link's boat has a limitation: the boat can only move in the same direction as the Wind. So, for instance, if the wind is blowing North, Link can only travel to the North. If the wind is not blowing at all, Link doesn't move at all, too. Fortunately, Link has the _wind waker_, the magical baton. With this baton, Link can conduct the _Wind's Requiem_, a mystical melody that allows Link to control the wind. Each time the wind waker is used, Link can either make the wind stop blowing (this action is represented by the letter X) or make the wind blow in one of the 8 cardinal directions (North (N), South (S), East (E), West (W), Northeast (NE), Southeast (SE), Southwest (SW), Northwest(NW)).  Link using the wind waker Link must go to the position (x $ _{2} $ ,y $ _{2} $ ) and stop there, to collect a legendary item. Right now, Link is at the position (x $ _{1} $ ,y $ _{1} $ ) and the wind is not blowing. You must find a trajectory from (x $ _{1} $ ,y $ _{1} $ ) to (x $ _{2} $ ,y $ _{2} $ ). A trajectory consists of a sequence of uses of the wind waker at certain positions. For example, to go from (0,0) to (1,1), a possible trajectory is: 1. At point (0,0), make the wind blow north; 2. At point (0,1), make the wind blow east; 3. At point (1,1), make the wind stop blowing. You must find a trajectory that: - Minimizes the number of times Link uses the wind waker; - In case of a tie, minimizes the total distance traveled; - In case of a tie, uses the lexicographically smaller sequence of wind direction changes. Use _E < N < NE < NW < S < SE < SW < W < X_. For example, a trajectory that changes the wind to N, then to SW, then to W is preferable over a trajectory that changes the wind to N, then to W, then to E, because _(N,NW,W)_ is lexicographically smaller than _(N,W,E)_ (because _N=N, NW < W_). Check the sample input and output. Note: The names "Link", "The Wind Waker" and some images above are copyrighted by **Nintendo (r)**. The author just wanted to make the problem more interesting. The author supports **Nintendo**!

The input file consists of one or more test cases. Each test case is described by a line containing four integers x $ _{1} $ , y $ _{1} $ , x $ _{2} $ , y $ _{2} $ (|x $ _{1} $ |, |y $ _{1} $ |, |x $ _{2} $ |, |y $ _{2} $ | The file ends with EOF.

For each test case, print a line containing K, the number of times the wind waker is used. In the next K lines print _x $ _{i} $ y $ _{i} $ D_, meaning that the wind waker must be used to change the wind direction to _D_ at the position _(x $ _{i} $ ,y $ _{i} $ )_. Print the coordinates rounded to exactly two fractional digits, and use _D_=_'S',N','W','E','SE','SW','NE','NW'_ or _'X'_. Print the events in the order they occur in the trajectory. After the _K_ lines, print the total distance traveled, rounded to exactly three fractional digits. Print a blank line after each test case. Check the sample output.