SP14932 LCA - Lowest Common Ancestor
题目描述
> 树是一种简单无向图,图中任意两个节点仅被一条边连接。所有连通无环无向图都是一棵树。
>
> 最近公共祖先(LCA)是图论和计算机科学中的一个概念。设 $\text{T}$ 是一个有 $N$ 个节点的有根树,树上有两个节点 $v$ 和 $w$,而这两个节点的最近公共祖先是 $u$,那么 $u$ 是 $v$ 和 $w$ 在 $\text{T}$ 上的祖先(允许自己是自己的祖先),且在满足上面的前提的所有节点中,其在 $T$ 上的高度最低。
>
>——摘自维基百科
现在,你需要对于给定的树 $\text{T}$ 以及两个节点 $v$ 和 $w$,求出它们的最近公共祖先。
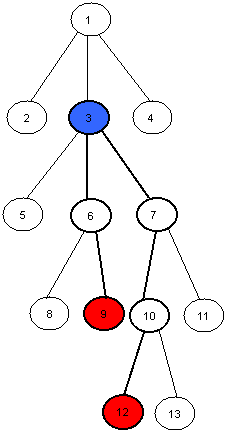
如下图所示,图中 $9$ 号节点与 $12$ 号节点的最近公共祖先为 $3$ 号节点。
输入格式
输入共有 $T$ 组数据。
对于每一组数据:
第一行输入一个整数 $N$ 表示节点个数(节点编号为 $1 \to N$ 中的一个数字)。
接下来 $N$ 行,每行开头是一个整数 $M_i$,表示 $i$ 号节点的子节点数量,后面的 $M_i$ 个整数分别表示子节点编号。
随后一行输入一个整数 $Q$,表示询问的 $v_i$ 及 $w_i$ 的组数。
最后 $Q$ 行,每行输入两个整数 $v_i$ 和 $w_i$,代表要询问的两个节点。
输出格式
输出共有 $T$ 组数据。
对于每一组数据:
第一行输出一个形如 `Case X:` 的字符串,其中的 `X` 表示第几组数据。
接下来 $Q$ 行(每组数据不一),输出每组 $v_i$ 和 $w_i$ 的最近公共祖先。
说明/提示
### 【样例 1 解释】
此样例在【题目描述】中有解释。
### 数据范围
对于 $100\%$ 的数据,$1 \le N \le 1000,0 \le M \le N - 1,1 \le Q \le 1000$。