SP14932 LCA - Lowest Common Ancestor

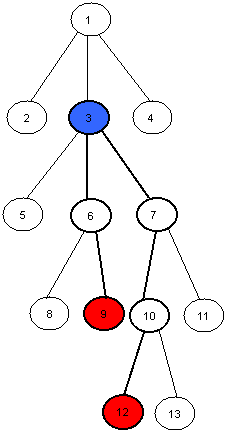
> 树是一种简单无向图，图中任意两个节点仅被一条边连接。所有连通无环无向图都是一棵树。 > > 最近公共祖先（LCA）是图论和计算机科学中的一个概念。设 $\text{T}$ 是一个有 $N$ 个节点的有根树，树上有两个节点 $v$ 和 $w$，而这两个节点的最近公共祖先是 $u$，那么 $u$ 是 $v$ 和 $w$ 在 $\text{T}$ 上的祖先（允许自己是自己的祖先），且在满足上面的前提的所有节点中，其在 $T$ 上的高度最低。 > >——摘自维基百科 现在，你需要对于给定的树 $\text{T}$ 以及两个节点 $v$ 和 $w$，求出它们的最近公共祖先。 如下图所示，图中 $9$ 号节点与 $12$ 号节点的最近公共祖先为 $3$ 号节点。 

输入共有 $T$ 组数据。 对于每一组数据： 第一行输入一个整数 $N$ 表示节点个数（节点编号为 $1 \to N$ 中的一个数字）。 接下来 $N$ 行，每行开头是一个整数 $M_i$，表示 $i$ 号节点的子节点数量，后面的 $M_i$ 个整数分别表示子节点编号。 随后一行输入一个整数 $Q$，表示询问的 $v_i$ 及 $w_i$ 的组数。 最后 $Q$ 行，每行输入两个整数 $v_i$ 和 $w_i$，代表要询问的两个节点。

输出共有 $T$ 组数据。 对于每一组数据： 第一行输出一个形如 `Case X:` 的字符串，其中的 `X` 表示第几组数据。 接下来 $Q$ 行（每组数据不一），输出每组 $v_i$ 和 $w_i$ 的最近公共祖先。

### 【样例 1 解释】 此样例在【题目描述】中有解释。 ### 数据范围 对于 $100\%$ 的数据，$1 \le N \le 1000,0 \le M \le N - 1,1 \le Q \le 1000$。