SP1801 DRINK - Drink, on Ice

一杯好的饮料通常都是经过冰镇的。也就是说，冰的含量至关重要。如果饮料中冰块很多的话，这杯饮料就会被很好的冰镇。但是，这种说法其实带有一点欺骗的成分，因为有时根本不需要那么多的冰来冰镇（比如杯子里省出来的地方可以放更多的伏特加）。然而假如冰的含量过少，这杯饮料就没有被冰镇了，令人难以下咽。 现在，酒吧的调酒师来寻求你的帮助——当然不是让你帮助调酒或者喝饮料——是让你算出这些饮料和冰混合后的预期产物。 为了简化问题，我们假设所有的饮料都是水，这些水和冰的混合发生在一个密闭系统中（不必考虑混合物和杯壁与外界发生的热传递）。这样一来，经过一段时间之后，该系统会达到一个稳定态（即温度不再改变，没有熔化和凝固的物态变化发生）。你需要求出这个系统达到稳定态时的温度，以及此时剩余水和冰的质量。 就像大家物理课上都学过的： - 水的比热容$c_水=4.19J/(g \cdot K)$，这意味着使质量为1g的水温度升高1开尔文所需要的能量是4.19焦耳 - 冰的比热容$c_冰=2.09J/(g \cdot K)$，这意味着使质量为1g的冰温度升高1开尔文所需要的能量是2.09焦耳。 - 冰的熔化热$\lambda_冰=335J/g$，这意味着使质量为1g的冰熔化需要335焦耳能量，且冰融化成水的过程中温度始终为$0 \degree C$。 - 反应开始前水和冰的内能总和等于反应结束后水和冰的内能总和。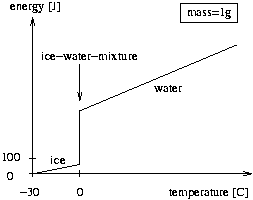 下面的图表说明了质量为1g的冰，冰水混合物，水相对于$-30 \degree C$的冰分别含有的内能。$0 \degree C$时的竖线表示冰的熔化，此时获得的内能和冰已经熔化的质量成正比。 

输入包含多组数据。 每一组数据包含四个实数$m_w, m_i, t_w, t_i$，分别代表水的质量，冰的质量，水的初始温度，冰的初始温度。 输入以`0 0 0 0`结束。

## 输入输出样例 __输入 #1__ ``` 100 20 50 -10 100 22 0 0 100 35 25 -10.5 10 90 25 -28 0 0 0 0 ``` __输出 #1__ ``` 0.0 g of ice and 120.0 g of water at 27.5 C 22.0 g of ice and 100.0 g of water at 0.0 C 6.0 g of ice and 129.0 g of water at 0.0 C 100.0 g of ice and 0.0 g of water at -4.2 C ``` ## 数据规模与约定 本题所有输入输出数据中的质量都应以克(g)为单位，温度都应以摄氏度(℃)为单位。 对于$100\%$的数据，$m_w \geqslant 0$，$m_i \geqslant 0$，$m_w + m_i > 0$，$-30 < t_i \leqslant 0 \leqslant t_w < 100$。 注：原题面中冰的熔化热采用的物理量符号是$e_冰$。