SP1815 WA - Problems Collection (Volume X)

These ten problems come from Chinese National Olympiad in Mathematics - Province Contest. **Problem 1** Polynomial P(x)=x $ ^{5} $ +a $ _{1} $ x $ ^{4} $ +a $ _{2} $ x $ ^{3} $ +a $ _{3} $ x $ ^{2} $ +a $ _{4} $ x+a $ _{5} $ , and we know when k=1, 2, 3, 4, P(k)=2007\*k. Calculate P(10)-P(-5). **Problem 2** The sum of 100 positive integers a $ _{1} $ , a $ _{2} $ , ..., a $ _{100} $ is 2007. Calculate the maximum possible value of 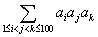. **Problem 3** Calculate 100101102103104......498499500 modulo 126. **Problem 4** We define the sum of the first n numbers of geometric progression {a $ _{n} $ } S $ _{n} $ . Now we know S $ _{7} $ =7, S $ _{14} $ =2014. Calculate S $ _{7} $ \*(S $ _{21} $ -S $ _{14} $ ). **Problem 5** Calculate the sum of this kind of positive integers n(n>=4): n satisfies that n! can be written as the product of n-3 consecutive positive integers. **Problem 6** Two vertices of a square are on the line y=2x-17, while the other two are on the parabola y=x $ ^{2} $ . Calculate the sum of two different possible values of the area of this square. **Problem 7** A, B, C, D are four fixed points in the space and they are not on the same plane. Calculate the number of different parallelepipeds, which satisfies that 4 vertices of the parallelepiped are A, B, C and D. **Problem 8** Polynomial x $ ^{2} $ -x-1 exactly divides Polynomial a $ _{1} $ x $ ^{17} $ +a $ _{2} $ x $ ^{16} $ +1. Calculate a $ _{1} $ \*a $ _{2} $ . **Problem 9** Suppose x is an acute angle, calculate the minimum possible value of (_sin_ x +_cos_ x)/(_sin_ x +_tan_ x) + (_tan_ x +_cot_ x)/(_cos_ x +_tan_ x) + (_sin_ x +_cos_ x)/(_cos_ x +_cot_ x) + (_tan_ x +_cot_ x)/(_sin_ x +_cot_ x). **Problem 10** Suppose x $ ^{4} $ +y $ ^{4} $ +z $ ^{4} $ =m/n, x, y, z are all real numbers, satisfying x\*y+y\*z+z\*x=1 and 5\*(x+1/x)=12\*(y+1/y)=13\*(z+1/z); m, n are positive integers and their greatest common divisor is 1. Calculate m+n.

There is no input.

Ten lines, each contains a single integer denoted the answer to the correspoding problem.